21 Cautions in hypothesis testing – I



Announcements

  • Today is the last day to hand in mini-project Phase 1 for credit.
  • Homework 7 (last homework!) & Mini-project Phase 2 are due one week from today, on Thursday, April 21. There will be class time to work on these today and all next week. Please use this time to minimize stress outside class!
  • Homework 7 is longer than usual (hence why you’ll have so much class time to consider it). It is an important broad, though not exhaustive, review of the semester!





21.1 Getting started

The whole point

  • We can use sample data to estimate features of the population.

  • There’s error in this estimation.

  • Taking this error into account, we want to make some sort of conclusion about the population.

  • There is some gray area in this conclusion and we might be wrong. NOTE: This includes but is not limited to the chance of making a Type I or Type II error (not because we did anything wrong, but because we got unlucky data which led to an incorrect conclusion).


. \(H_0\) true \(H_0\) not true
conclude results aren’t significant Correct! Type II Error (false negative)
conclude results are significant Type I Error (false positive) Correct!





WARM-UP

What can we conclude about the association of mountain climber success with their age, their oxygen use, the height of their climb, and whether or not they did the hike solo (as opposed to in a team)? What type of errors might we be making?

# Load packages and data
library(dplyr)
library(ggplot2)
climbers <- read.csv("https://www.macalester.edu/~ajohns24/data/climbers_sub.csv")

# Build the model of success
climb_model <- glm(success ~ age + oxygen_used, climbers, family = "binomial")
coef(summary(climb_model))
##                    Estimate  Std. Error   z value      Pr(>|z|)
## (Intercept)     -0.51957247 0.207331212 -2.506002  1.221049e-02
## age             -0.02197407 0.005459778 -4.024718  5.704361e-05
## oxygen_usedTRUE  2.89559690 0.126370801 22.913496 3.408591e-116

# Check out the confidence intervals
confint(climb_model)
##                       2.5 %      97.5 %
## (Intercept)     -0.92682316 -0.11372877
## age             -0.03275496 -0.01134335
## oxygen_usedTRUE  2.65182522  3.14753145
exp(confint(climb_model))
##                      2.5 %     97.5 %
## (Intercept)      0.3958091  0.8925000
## age              0.9677757  0.9887207
## oxygen_usedTRUE 14.1798965 23.2785293





21.2 Exercises

Directions

  • Explore common abuses of hypothesis testing so that (1) you don’t make these mistakes yourself; and (2) you can read others’ work with a healthy critical eye.
  • Review. The exercises focus on new concepts, yet they require the understanding of “old” material. Though you won’t be required to do so, make sure you could write down model formulas, make predictions, interpret coefficients, etc if asked.



  1. Warm-up: gray area
    Scroll down and check out the list in this article. Why is this funny?



  1. The claim
    Two researchers make a claim: songs in the latin genre are longer than those in the pop / edm genres. Thus they’re interested in the population model of song duration (in seconds) by latin_genre:

    duration = \(\beta_0\) + \(\beta_1\) latin_genreTRUE

    where population coefficients \(\beta_0\) and \(\beta_1\) are unknown. Which set of hypotheses align with the researchers’ claim?

    • \(H_0\): \(\beta_1 = 0\) vs \(H_a\): \(\beta_1 < 0\)
    • \(H_0\): \(\beta_1 = 0\) vs \(H_a\): \(\beta_1 \ne 0\)
    • \(H_0\): \(\beta_1 = 0\) vs \(H_a\): \(\beta_1 > 0\)



  1. Researcher 1
    To test these hypotheses, Researcher 1 collects data on 20 songs and uses this to model song duration (in seconds) by latin_genre:

    # Load the data
spotify_small <- read.csv("https://www.macalester.edu/~ajohns24/data/spotify_example_small.csv") %>% 
  select(track_artist, track_name, duration_ms, latin_genre) %>% 
  mutate(duration = duration_ms / 1000)

# Construct the model
spotify_model_1 <- lm(duration ~ latin_genre, spotify_small)
coef(summary(spotify_model_1))
##                  Estimate Std. Error  t value     Pr(>|t|)
## (Intercept)     214.99869   12.97571 16.56932 2.412163e-12
## latin_genreTRUE  39.45606   29.01458  1.35987 1.906619e-01

    1. Using the 68-95-99.7 Rule and confint(), construct an approximate 95% confidence interval for the actual latin_genre population coefficient \(\beta_1\).

    2. Interpret your CI from part a.

    3. Using this confidence interval alone, what conclusion do you make about the hypotheses?

      • We have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.
      • We do not have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.



  1. Researcher 2 – part 1
    Researcher 2 has the same research question, but gathers a different set of data:

    spotify_big <- read.csv("https://www.macalester.edu/~ajohns24/data/spotify_example_big.csv") %>% 
  select(track_artist, track_name, duration_ms, latin_genre) %>% 
  mutate(duration = duration_ms / 1000)
    1. How many songs did Researcher 2 collect in spotify_big?
    2. Using the spotify_big data, construct and comment on a visualization of the relationship between duration and latin_genre.



  1. Researcher 2 – part 2
    Using Researcher 2’s data, let’s model duration by latin_genre:

    # Construct the model
spotify_model_2 <- lm(duration ~ latin_genre, spotify_big)
coef(summary(spotify_model_2))
##                   Estimate Std. Error   t value   Pr(>|t|)
## (Intercept)     212.673908  0.4165491 510.56143 0.00000000
## latin_genreTRUE   1.555355  0.7435700   2.09174 0.03647731

    1. Interpret the latin_genreTRUE coefficient.

    2. In the context of song listening, is this a large or small effect size?



  1. Researcher 2 – part 3
    Let’s conclude Researcher 2’s analysis.
    1. Report the p-value for the researcher’s hypothesis test (H_a: the latin_genreTRUE coefficient is positive).
    2. How can we interpret this p-value “p”?
      • There’s only a p% chance that latin genre songs tend to be longer than pop / edm songs.
      • If there were truly no difference in the duration of latin vs pop / edm songs (in the broader population of songs), there’s only a p% chance that we’d have gotten a sample in which the observed difference was so large.
      • There’s only a p% chance that latin genre songs tend to be the same length as pop / edm songs.
    3. If the researchers made a yes-or-no decision using a 0.05 significance level, what would they say?
      • We have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.
      • We do not have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.



  1. Reflection
    HUH?!? You’ve just witnessed the stark difference between statistical significance and practical significance. Explain why this happened. That is, when might we observe statistically significant results that aren’t practically significant?
    NOTE:
    • This result is consistent with our exploration of Type II error rates.
    • This result seems silly, but is quite common in practice. Hence it emphasizes the importance of investigating statistical and practical significance hand-in-hand.





21.3 Solutions

  1. Warm-up: gray area



  1. The claim
    \(H_0\): \(\beta_1 = 0\) vs \(H_a\): \(\beta_1 > 0\)



  1. Researcher 1

    # Load the data
spotify_small <- read.csv("https://www.macalester.edu/~ajohns24/data/spotify_example_small.csv") %>% 
  select(track_artist, track_name, duration_ms, latin_genre) %>% 
  mutate(duration = duration_ms / 1000)

# Construct the model
spotify_model_1 <- lm(duration ~ latin_genre, spotify_small)
coef(summary(spotify_model_1))
##                  Estimate Std. Error  t value     Pr(>|t|)
## (Intercept)     214.99869   12.97571 16.56932 2.412163e-12
## latin_genreTRUE  39.45606   29.01458  1.35987 1.906619e-01

    1. .

      39.45606 - 2*29.01458
## [1] -18.5731
39.45606 + 2*29.01458
## [1] 97.48522
confint(spotify_model_1)
##                    2.5 %   97.5 %
## (Intercept)     187.7377 242.2596
## latin_genreTRUE -21.5013 100.4134

    2. We’re 95% confident that the average duration of latin genre songs is somewhere between 21.5 shorter and 100.4 seconds longer than the edm / pop genre.

    3. We do not have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.



  1. Researcher 2 – part 1

    spotify_big <- read.csv("https://www.macalester.edu/~ajohns24/data/spotify_example_big.csv") %>% 
  select(track_artist, track_name, duration_ms, latin_genre) %>% 
  mutate(duration = duration_ms / 1000)

    1. .

      nrow(spotify_big)
## [1] 16216

    2. There appears to be very little difference in the duration among the genres.

      ggplot(spotify_big, aes(x = duration, color = latin_genre)) + 
  geom_density()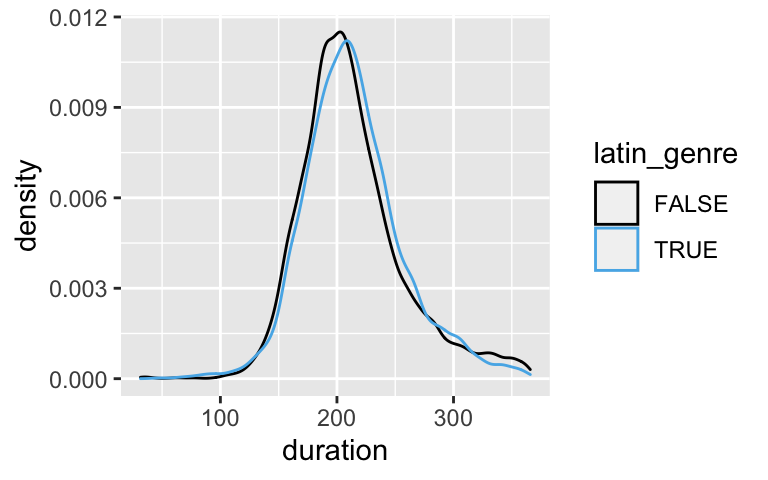



  1. Researcher 2 – part 2

    # Construct the model
spotify_model_2 <- lm(duration ~ latin_genre, spotify_big)
coef(summary(spotify_model_2))
##                   Estimate Std. Error   t value   Pr(>|t|)
## (Intercept)     212.673908  0.4165491 510.56143 0.00000000
## latin_genreTRUE   1.555355  0.7435700   2.09174 0.03647731

    1. On average, latin genre songs tend to be 1.56 seconds longer than edm / pop songs

    2. No!



  1. Researcher 2 – part 3
    1. 0.03647731 / 2 = 0.018
    2. If there were truly no difference in the duration of latin vs pop / edm songs (in the broader population of songs), there’s only a p% chance that we’d have gotten a sample in which the observed difference was so large.
    3. We have statistically significant evidence that latin genre songs tend to be longer than pop / edm songs.



  1. Reflection
    Large sample size! The more data we have, the smaller our standard errors. Thus the narrower our CIs and the smaller our p-values. Thus the easier it is to establish statistical significance even when the results aren’t practically significant.