16 Normal model + random samples

in experiment exercises, first plot the model lines, then the sampling distributions of the intercepts and slopes

Announcements

Sit with at least a couple new people today! Introduce yourselves.
Checkpoint 13 is due Tuesday. There’s no homework next week, but if you haven’t yet handed in Homework 5, it’s due Tuesday by 9:30am.
If you don’t yet have a group for the mini-project, it’s important to figure that out soon. Working alone is not an option. If you’re stumped, reach out to me this week.
Quiz 2 is next Thursday. It is the same format as Quiz 1, it is (necessarily) cumulative, and it will cover material up through logistic regression (not today’s material!). The following are some of the bigger concepts on the quiz: Normal vs logistic regression, multicollinearity, interaction (what it means and how to interpret an interaction coefficient), interpreting model coefficients (Normal and logistic), making predictions (Normal and logistic), evaluating logistic regression models, R-squared.
I’m appreciative of the people who have been speaking up in class and am hoping that more start feeling comfortable sharing their thoughts. It’s important to hear from more of you! Just a heads up that if this doesn’t happen naturally, I’ll call on different tables (not individuals) to share their thoughts.

16.1 Getting started

Today marks a significant shift in the semester. Thus far, we’ve focused on exploratory analysis: visualizations, numerical summaries, and models that capture the patterns in our sample data. Today, we’ll move on to inference: using our data to make conclusions about the broader population from which it was taken:

Goals for today

Explore the Normal probability model, a tool we’ll need to turn information in our sample data into inferences about the broader population.
Run a little class experiment to consider the ideas of randomness, sample estimation, and how they connect to the Normal model.

16.2 Experiment

Github user Tony McGovern has compiled and made available presidential election results for the population of all 3000+ U.S. counties (except Alaska). (Image: Wikimedia Commons)

Import the combined and slightly wrangled data:

# Load packages and import and wrangle data
library(dplyr)
library(ggplot2)
elections <- read.csv("https://www.macalester.edu/~ajohns24/data/election_2020.csv") %>% 
  mutate(per_gop_2020 = 100*per_gop_2020, 
    per_gop_2016 = 100*per_gop_2016, per_gop_2012 = 100*per_gop_2012)

The Republican (or “GOP”) candidate for president was Donald Trump in 2020 and Mitt Romney in 2012. Our goal will be to understand how Trump’s 2020 vote percentage (per_gop_2020) relates to Romney’s 2012 vote percentage (per_gop_2012). BUT let’s pretend that we’re working within the typical scenario - we don’t have access to the entire population of interest. Instead, we need to estimate population trends using data from a randomly selected sample of counties.

Sampling & randomness in RStudio
We’ll be taking some random samples of counties throughout this activity. The underlying random number generator plays a role in the random sample we happen to get:
```
# Try the following chunk A FEW TIMES
sample_n(elections, size = 2, replace = FALSE)
```
```
# Try the following FULL chunk A FEW TIMES
set.seed(155)
sample_n(elections, size = 2, replace = FALSE)
```
NOTE: If we set.seed(some positive integer) before taking a random sample, we’ll get the same results. This reproducibility is important:
- we get the same results every time we knit the Rmd
- we can share our work with others & ensure they get our same answers
- it wouldn’t be great if you submitted your work to, say, a journal and weren’t able to back up / confirm / reproduce your results!

Take your own sample
1. Set your own random number seed to your own phone number – just the numbers so that you have a 7-digit or 10-digit integer. (The number isn’t important. What’s important is that your number is different than other students’.)
```
set.seed(YOURSEED)
```
2. Take a random sample of 10 counties:
```
my_sample <- sample_n(elections, size = 10, replace = FALSE)
my_sample                       
```
3. Calculate the average percentage of votes that Trump won in your 10 sample counties.
```
my_sample %>% 
  summarize(mean(per_gop_2020))
```
4. Construct and plot your model of Trump’s 2020 vs 2012 vote percentage:
```
ggplot(my_sample, aes(x = per_gop_2012, y = per_gop_2020)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE)

my_model <- lm(per_gop_2020 ~ per_gop_2012, my_sample)
coef(summary(my_model))
```

Report your work
Indicate your sample mean, intercept, and slope estimates in this survey. You’ll come back to analyze this experiment data later in the activity!

16.3 Exercises: Normal model

In this section you will practice the concepts you explored in today’s video. First, run the following code which defines a shaded_normal() function which is specialized to this activity alone:

shaded_normal <- function(mean, sd, a = NULL, b = NULL){
  min_x <- mean - 4*sd
  max_x <- mean + 4*sd
  a <- max(a, min_x)
  b <- min(b, max_x)
  ggplot() + 
    scale_x_continuous(limits = c(min_x, max_x), breaks = c(mean - sd*(0:3), mean + sd*(1:3))) +
    stat_function(fun = dnorm, args = list(mean = mean, sd = sd)) + 
    stat_function(geom = "area", fun = dnorm, args = list(mean = mean, sd = sd), xlim = c(a, b), fill = "blue") + 
    labs(y = "density")
}

A Normal model
Suppose that the speeds of cars on a highway, in miles per hour, can be reasonably represented by the following model: N(55, 5²).
1. What are the mean speed and standard deviation in speeds from car to car?
2. Plot this Normal model.
```
# shaded_normal(mean = ___, sd = ___)
```

68-95-99.7 Rule
1. Provide the range of the middle 68% of speeds and shade in the corresponding region on your Normal curve. NOTE: a is the lower end of the range and b is the upper end.
```
# shaded_normal(mean = ___, sd = ___, a = ___, b = ___)
```
2. Repeat part a for the middle 95%.
3. Repeat part a for the middle 99.7%.

Calculate probabilities
We can also use the 68-95-99.7 Rule to calculate probabilities!
1. Calculate the probability that a car’s speed exceeds 60mph. The following plot can provide some intuition:
```
shaded_normal(mean = 55, sd = 5, a = 60)
```
2. Calculate the probability that a car will be traveling at less than 45mph.
```
shaded_normal(mean = 55, sd = 5, b = 45)
```
3. Calculate the probability that a car will be traveling at less than 40mph.
```
shaded_normal(mean = 55, sd = 5, b = 40)
```

Approximate probabilities
Speeds don’t always fall exactly in increments of 5mph (the standard deviation) from the mean of 55mph. Though we can use other tools to calculate probabilities in these scenarios, the 68-95-99.7 Rule can still provide insight. For each scenario below, indicate which range the probability falls into: less than 0.0015, between 0.0015 and 0.025, between 0.025 and 0.16, or greater than 0.16.
1. the probability that a car’s speed exceeds 57mph
```
shaded_normal(mean = 55, sd = 5, a = 57)
```
2. the probability that a car’s speed exceeds 67mph
```
shaded_normal(mean = 55, sd = 5, a = 67)
```
3. the probability that a car’s speed exceeds 71mph
```
shaded_normal(mean = 55, sd = 5, a = 71)
```

Z scores
Inherently important to all of our calculations above is how many standard deviations a value “X” is from the mean. This distance is called a Z-score and can be calculated as follows:

(X - mean) / sd

For example, if I’m traveling 40 miles an hour, my Z-score is -3. That is, my speed is 3 standard deviations below the average speed:
```
(40 - 55) / 5
## [1] -3
```
1. Driver A is traveling at 60mph on the highway where speeds are N(55, 5²) and the speed limit is 55mph. Calculate and interpret their Z-score.
2. Driver B is traveling at 36mph on a residential road where speeds are N(30, 3²) and the speed limit is 30mph. Calculate and interpret their Z-score.
3. Both drivers are speeding, though in different scenarios (highway vs residential). Who is speeding more? Explain. NOTE: The following plots might provide some insights:
```
# Driver A
shaded_normal(mean = 55, sd = 5) + 
  geom_vline(xintercept = 60)

# Driver B
shaded_normal(mean = 30, sd = 3) + 
  geom_vline(xintercept = 36)  
```

16.4 Exercises: Random samples

The Normal exercises above are directly relevant to using our sample data to learn about the broader population of interest. Let’s see where these two ideas connect!

Comparing mean estimates (part 1)
Recall that each student took a sample of 10 U.S. counties. From this sample, you each estimated Trump’s mean 2020 support and the relationship between Trump’s 2020 results and Romney’s 2012 results. Import the resulting sample_mean, sample_intercept, and sample_slope values:
```
results <- read.csv("https://www.macalester.edu/~ajohns24/data/election_simulation.csv")
names(results) <- c("time", "sample_mean", "sample_intercept", "sample_slope")
```
1. Construct and describe a density plot of the sample_mean values, i.e. each student’s sample estimate of Trump’s average support. What’s the typical estimate? The range in estimates? The shape of the density plot (does it look Normal-ish)?
```
ggplot(results, aes(x = sample_mean)) + 
  geom_density()
```
2. For more specific insight into the typical estimate of Trump’s mean support and the variability in the estimates from student to student, calculate the mean and standard deviation of the sample_mean values:
```
#results %>% 
#  ___(mean(sample_mean), sd(sample_mean))
```
3. Based on parts a and b, what do you think is the actual mean Trump support among all counties? What’s your reasoning?
4. Check your intuition. Calculate the mean Trump support across all counties. How does this compare to the typical sample estimate?
```
#elections %>%  
#  ___(mean(per_gop_2020))
```

Comparing mean estimates (part 2)
In the previous exercise, you observed that the collection of our sample mean estimates is Normally distributed around Trump’s actual mean support.
1. What was your sample estimate of Trump’s mean support?
2. How many percentage points was your estimate from Trump’s actual mean support?
3. How many standard deviations was your estimate from Trump’s actual mean support? That is, what’s your Z-score?

Comparing model estimates
Next, let’s examine how our sample estimates of the relationship between Trump’s 2020 support and Romney’s 2012 support varied from student to student.
1. Construct and describe density plots of the sample_intercept and sample_slope values. (Do these look Normal-ish?)
```
ggplot(results, aes(x = sample_intercept)) + 
  geom_density()
ggplot(results, aes(x = sample_slope)) + 
  geom_density()
```
2. Plot the sample model lines. How do these compare to the actual trend among all counties (red)?
```
ggplot(elections, aes(x = per_gop_2012, y = per_gop_2020)) +
  geom_abline(data = results, aes(intercept = sample_intercept, slope = sample_slope), color = "gray") + 
  geom_smooth(method = "lm", color = "red", se = FALSE)
```

Reflection
Reflect upon the exercises above. Summarize what you’ve learned about using sample data to estimate features of a broader population. For example:
- What model might describe how estimates behave from sample to sample?
- Though estimates can vary from sample to sample, around what value do the estimates center?

Data drill!

# What was Trump's lowest vote percentage?


# The highest?


# Show the state_name, county_name, and per_gop_2020 of the 6 counties where Trump had the lowest support


# Show the state_name, county_name, and per_gop_2020 of the 6 counties where Trump had the highest support


# What was Trump's lowest vote percentage in Minnesota? In what county was this?


# The highest?


# Construct and comment on a plot of voter turnout
# in 2020 (total_votes_2020) vs 2016 (total_votes_2016)
# For reference, add on a geom_abline(intercept = 0, slope = 1)


# What other questions do you have?

16.5 Optional: mapping!

Visualizing the election results on an actual map can provide some intuition for our work. To make maps, load the following package. NOTE: You’ll likely need to install this package first.

library(socviz)

Now process the data to include mapping info (eg: latitude and longitude coordinates):

mapping_data <- elections %>% 
  dplyr::rename(id = county_fips) %>% 
  mutate(id = as.character(id)) %>% 
  mutate(id = ifelse(nchar(id) == 4, paste0("0",id), id)) %>% 
  left_join(county_map, elections, by = "id")

Now make some maps!

ggplot(mapping_data, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA)

ggplot(mapping_data, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA) + 
  scale_fill_gradientn(colours = c("blue", "purple", "red"))

mn <- mapping_data %>% 
  filter(state_name == "Minnesota")
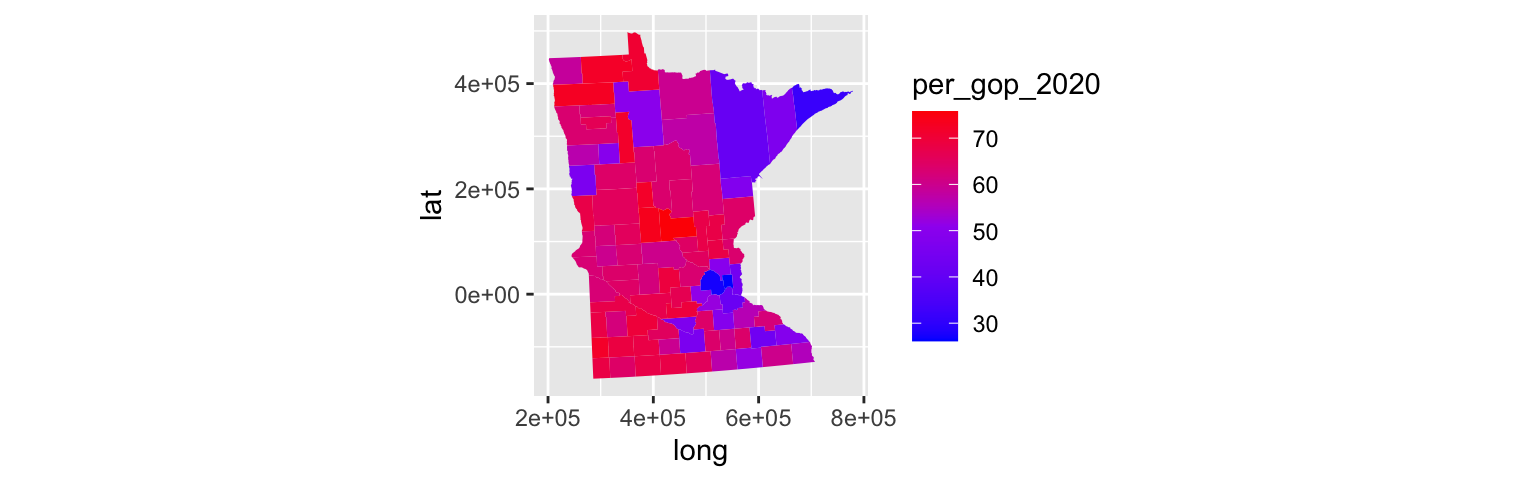
ggplot(mn, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA) + 
  scale_fill_gradientn(colours = c("blue", "purple", "red"), values = scales::rescale(seq(0, 100, by = 10)))

Play around!

Check out another state.
Plot the results of a different election.
Define and map a new variable that looks at the difference between per_gop_2020 and per_gop_2016 (ie. how did Trump’s support shift from 2016 to 2020?).

16.6 Solutions

Sampling & randomness in RStudio

# Try the following chunk A FEW TIMES
# NOTE: This is different every time
sample_n(elections, size = 2, replace = FALSE)
##   state_name state_abbr     county_name county_fips votes_gop_2020
## 1       Iowa         IA   Clarke County       19039           3144
## 2     Kansas         KS Mitchell County       20123           2454
##   votes_dem_2020 total_votes_2020 per_gop_2020 per_dem_2020 per_point_diff_2020
## 1           1466             4670     67.32334    0.3139186           0.3593148
## 2            547             3039     80.75025    0.1799934           0.6275090
##   votes_dem_2016 votes_gop_2016 total_votes_2016 per_dem_2016 per_gop_2016
## 1           1463           2706             4405    0.3321226     61.43019
## 2            469           2216             2824    0.1660765     78.47025
##   per_point_diff_2016 total_votes_2012 votes_dem_2012 votes_gop_2012
## 1          -0.2821793             4398           2187           2124
## 2          -0.6186261             2923            576           2293
##   per_dem_2012 per_gop_2012 per_point_diff_2012
## 1    0.4972715     48.29468          0.01432469
## 2    0.1970578     78.44680         -0.58741020

# Try the following FULL chunk A FEW TIMES
# NOTE: This is the same different every time
set.seed(155)
sample_n(elections, size = 2, replace = FALSE)
##   state_name state_abbr     county_name county_fips votes_gop_2020
## 1      Texas         TX   Baylor County       48023           1494
## 2    Indiana         IN Dearborn County       18029          19528
##   votes_dem_2020 total_votes_2020 per_gop_2020 per_dem_2020 per_point_diff_2020
## 1            183             1702     87.77908    0.1075206           0.7702703
## 2           5446            25383     76.93338    0.2145530           0.5547808
##   votes_dem_2016 votes_gop_2016 total_votes_2016 per_dem_2016 per_gop_2016
## 1            191           1267             1492    0.1280161     84.91957
## 2           4883          18110            23910    0.2042242     75.74237
##   per_point_diff_2016 total_votes_2012 votes_dem_2012 votes_gop_2012
## 1          -0.7211796             1592            267           1297
## 2          -0.5531995            22352           6527          15391
##   per_dem_2012 per_gop_2012 per_point_diff_2012
## 1    0.1677136     81.46985          -0.6469849
## 2    0.2920097     68.85737          -0.3965641

Take your own sample
Answers will vary

Report your work

A Normal model
1. mean = 55mph, sd = 5mph
2. .
```
shaded_normal(mean = 55, sd = 5)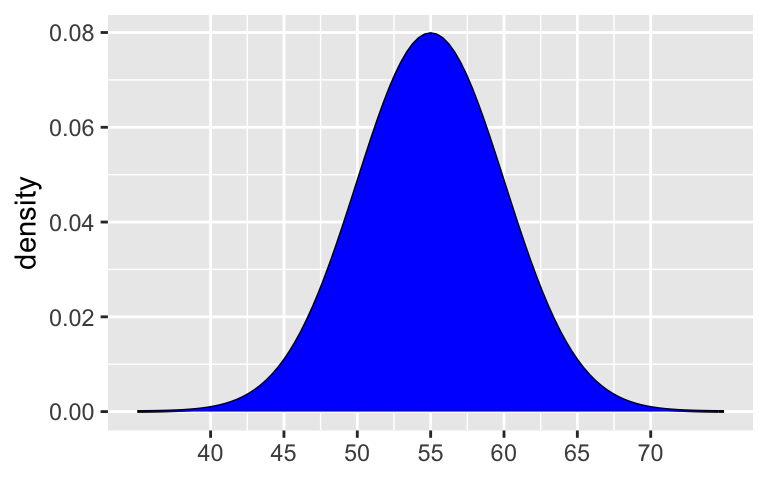
```

68-95-99.7 Rule

55 \(\pm\) 5 = (50, 60)

shaded_normal(mean = 55, sd = 5, a = 50, b = 60)

95%: 55 \(\pm\) 25 = (45, 65)
99.7%: 55 \(\pm\) 35 = (40, 70)

shaded_normal(mean = 55, sd = 5, a = 45, b = 65)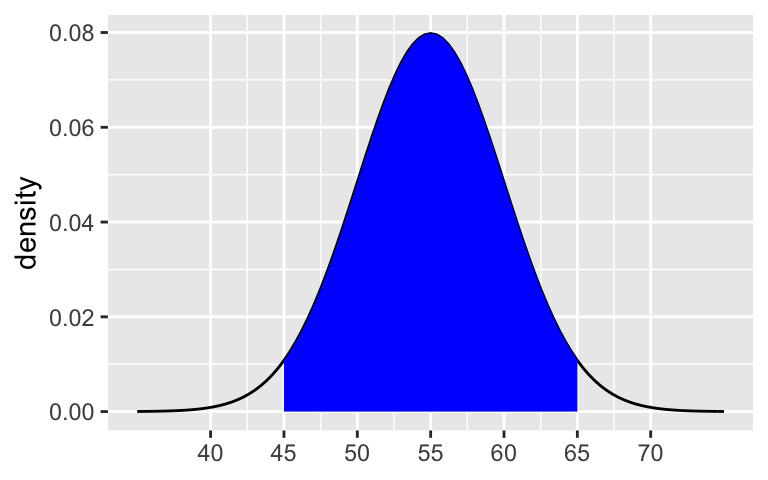

shaded_normal(mean = 55, sd = 5, a = 40, b = 70)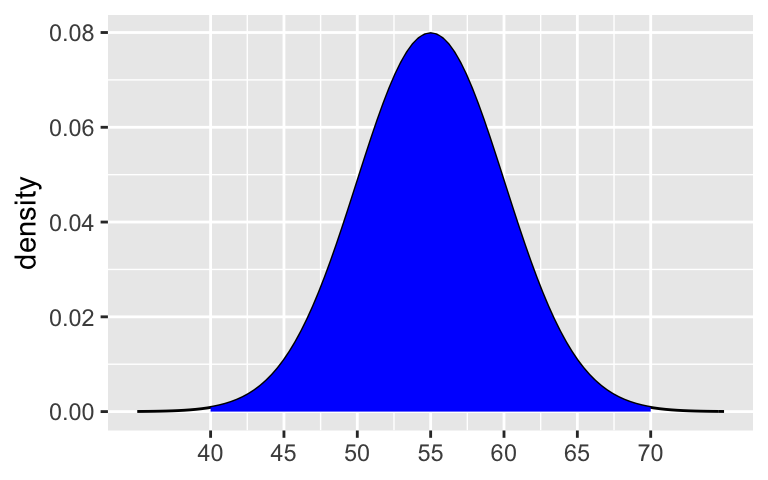

Calculate probabilities
1. 0.16. NOTE: There’s a 32% chance that a speed is outside the 50 to 60 range, split evenly between the 2 tails.
```
shaded_normal(mean = 55, sd = 5, a = 60)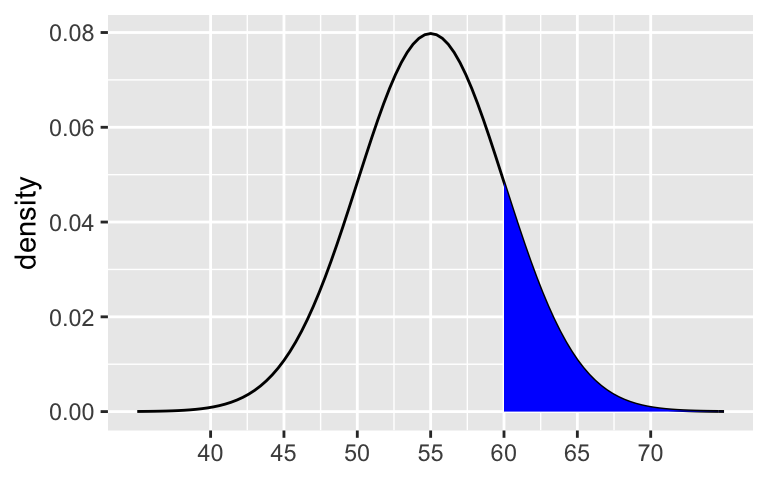
```
2. 0.025. NOTE: There’s a 5% chance that a speed is outside the 45 to 65 range, split evenly between the 2 tails.
```
shaded_normal(mean = 55, sd = 5, b = 45)
```
3. 0.0015. NOTE: There’s a 0.3% chance that a speed is outside the 40 to 70 range, split evenly between the 2 tails.
```
shaded_normal(mean = 55, sd = 5, b = 40)
```

Approximate probabilities
1. greater than 0.16. 57 is less than 1sd away from 55 (between 55 and 60).
```
shaded_normal(mean = 55, sd = 5, a = 57)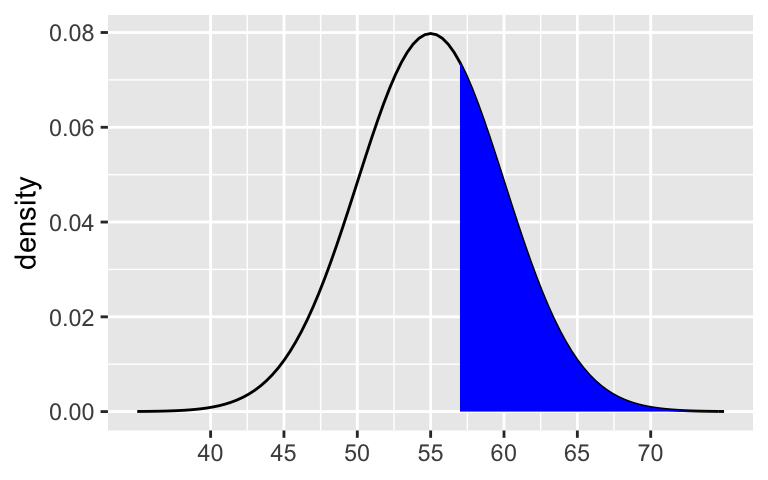
```
2. between 0.0015 and 0.025. 67 is between 2sd and 3sd away from 55 (between 65 and 70).
```
shaded_normal(mean = 55, sd = 5, a = 67)
```
3. less than 0.0015. 71 is more than 3sd away from 55 (greater than 70).
```
shaded_normal(mean = 55, sd = 5, a = 71)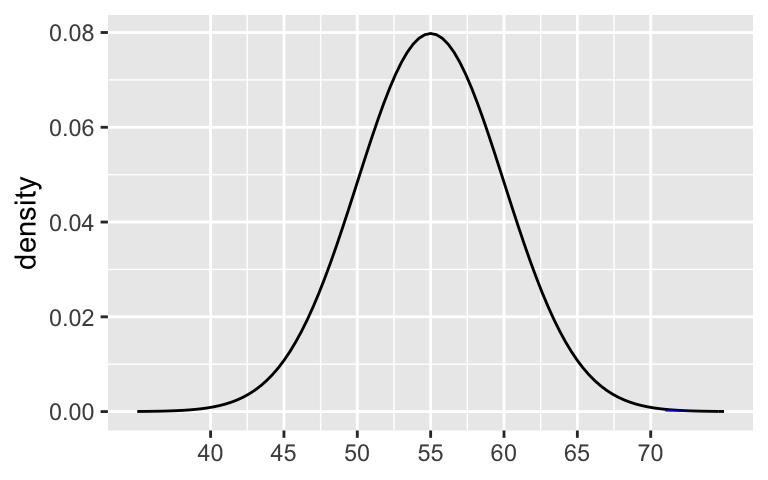
```

Z scores

Driver A is going 1sd above the speed limit.
```
(60 - 55) / 5
## [1] 1
```
Driver B is going 2sd above the speed limit.
```
(36 - 30) / 3
## [1] 2
```

Driver B. They’re going 2sd above the limit.

# Driver A
shaded_normal(mean = 55, sd = 5) + 
  geom_vline(xintercept = 60)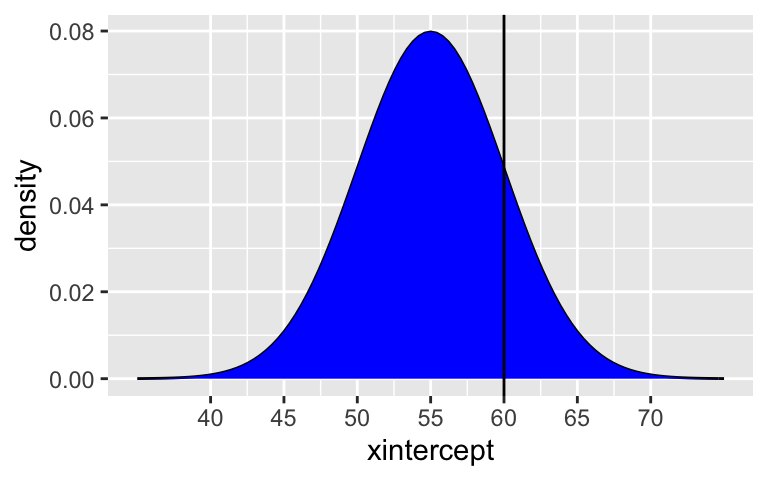


# Driver B
shaded_normal(mean = 30, sd = 3) + 
  geom_vline(xintercept = 36)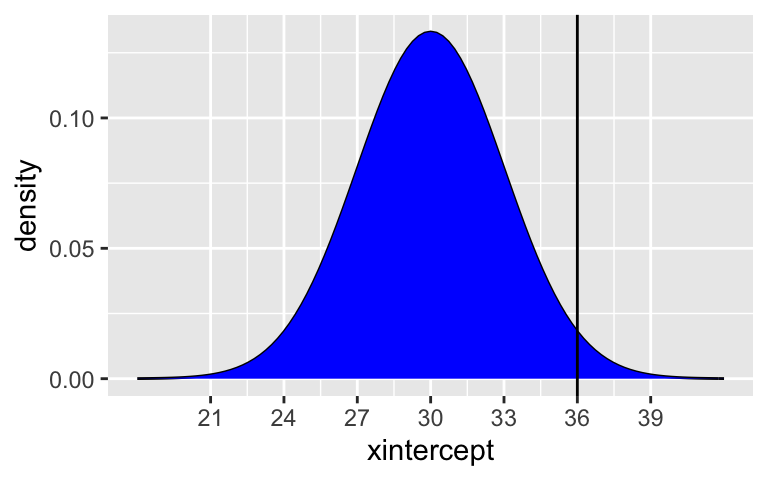

Comparing mean estimates (part 1)

results <- read.csv("https://www.macalester.edu/~ajohns24/data/election_simulation.csv")
names(results) <- c("time", "sample_mean", "sample_intercept", "sample_slope")

These are roughly Normal (bell-shaped) centered around 65 and ranging from roughly 51 to 75.
```
ggplot(results, aes(x = sample_mean)) + 
  geom_density()
```

results %>% 
  summarize(mean(sample_mean), sd(sample_mean))
##   mean(sample_mean) sd(sample_mean)
## 1          64.61347        5.470135

Will vary.

The actual mean is close to the center of the sample mean estimates.

elections %>% 
  summarize(mean(per_gop_2020))
##   mean(per_gop_2020)
## 1           64.99124

Comparing mean estimates (part 1)
Will vary depending upon your sample mean estimate.

Comparing model estimates

These look Normal-ish.

ggplot(results, aes(x = sample_intercept)) + 
  geom_density()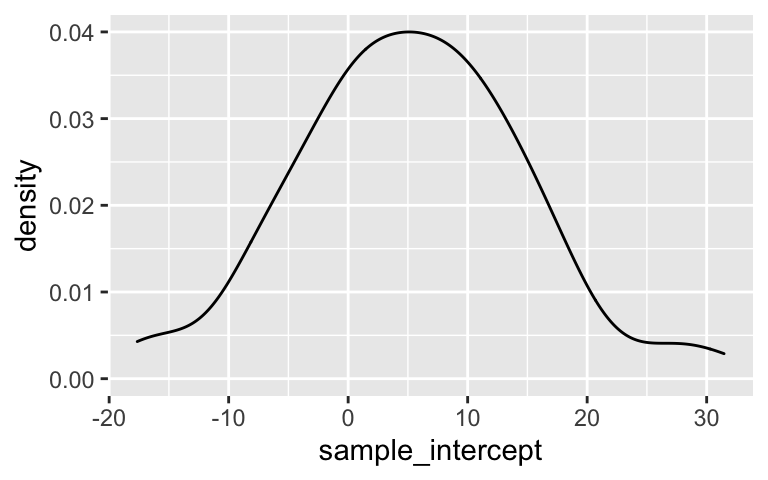

ggplot(results, aes(x = sample_slope)) + 
  geom_density()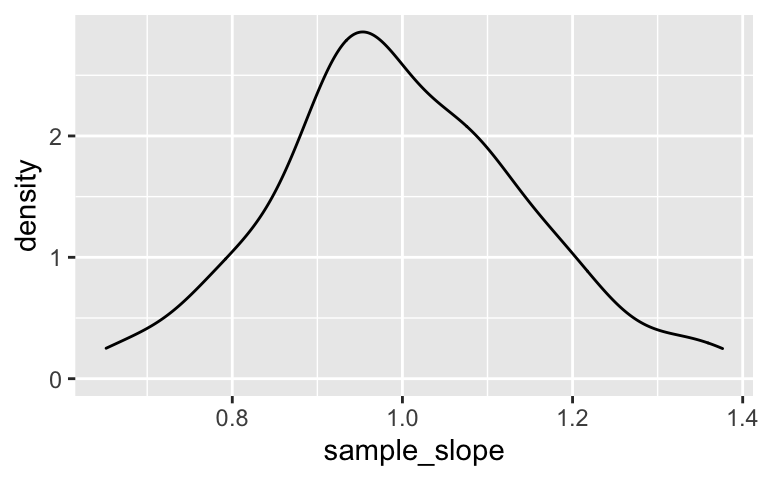

The actual trend is in the “middle” of the sample trends.

ggplot(elections, aes(x = per_gop_2012, y = per_gop_2020)) +
  geom_abline(data = results, aes(intercept = sample_intercept, slope = sample_slope), color = "gray") + 
  geom_smooth(method = "lm", color = "red", se = FALSE)

Will vary.

actual_trend <- lm(per_gop_2020 ~ per_gop_2012, elections)
coef(summary(actual_trend))
##              Estimate  Std. Error   t value     Pr(>|t|)
## (Intercept)  5.179393 0.486313057  10.65033 4.860116e-26
## per_gop_2012 1.000235 0.007896805 126.66328 0.000000e+00

Reflection

Optional but encouraged data drill

# What was Trump's lowest vote percentage?
elections %>% 
  summarize(min(per_gop_2020))
##   min(per_gop_2020)
## 1          5.397321

# The highest?
elections %>% 
  summarize(max(per_gop_2020))
##   max(per_gop_2020)
## 1          96.18182

# Show the state_name, county_name, and per_gop_2020 of the 6 counties where Trump had the lowest support
elections %>% 
  arrange(per_gop_2020) %>% 
  select(state_name, county_name, per_gop_2020) %>% 
  head()
##             state_name            county_name per_gop_2020
## 1 District of Columbia   District of Columbia     5.397321
## 2             Maryland Prince George's County     8.730037
## 3             Maryland         Baltimore city    10.685544
## 4             Virginia        Petersburg city    11.219720
## 5             New York        New York County    12.258528
## 6           California   San Francisco County    12.722062

# Show the state_name, county_name, and per_gop_2020 of the 6 counties where Trump had the highest support
elections %>% 
  arrange(desc(per_gop_2020)) %>% 
  select(state_name, county_name, per_gop_2020) %>% 
  head()
##   state_name      county_name per_gop_2020
## 1      Texas   Roberts County     96.18182
## 2      Texas    Borden County     95.43269
## 3      Texas      King County     94.96855
## 4    Montana  Garfield County     93.97294
## 5      Texas Glasscock County     93.56815
## 6   Nebraska     Grant County     93.28358

# What was Trump's lowest vote percentage in Minnesota? In what county was this?
elections %>% 
  filter(state_name == "Minnesota") %>% 
  arrange(per_gop_2020) %>% 
  select(state_name, county_name, per_gop_2020) %>% 
  head(1)
##   state_name   county_name per_gop_2020
## 1  Minnesota Ramsey County     26.14257


# The highest?
elections %>% 
  filter(state_name == "Minnesota") %>% 
  arrange(desc(per_gop_2020)) %>% 
  select(state_name, county_name, per_gop_2020) %>% 
  head(1)
##   state_name     county_name per_gop_2020
## 1  Minnesota Morrison County     75.77973


# Construct and comment on a plot of voter turnout
# in 2020 (total_votes_2020) vs 2016 (total_votes_2016)
# For reference, add on a geom_abline(intercept = 0, slope = 1)
ggplot(elections, aes(x = total_votes_2016, y = total_votes_2020)) + 
  geom_point() + 
  geom_abline(intercept = 0, slope = 1)

OPTIONAL MAPS

library(socviz)

mapping_data <- elections %>% 
  dplyr::rename(id = county_fips) %>% 
  mutate(id = as.character(id)) %>% 
  mutate(id = ifelse(nchar(id) == 4, paste0("0",id), id)) %>% 
  left_join(county_map, elections, by = "id")

ggplot(mapping_data, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA)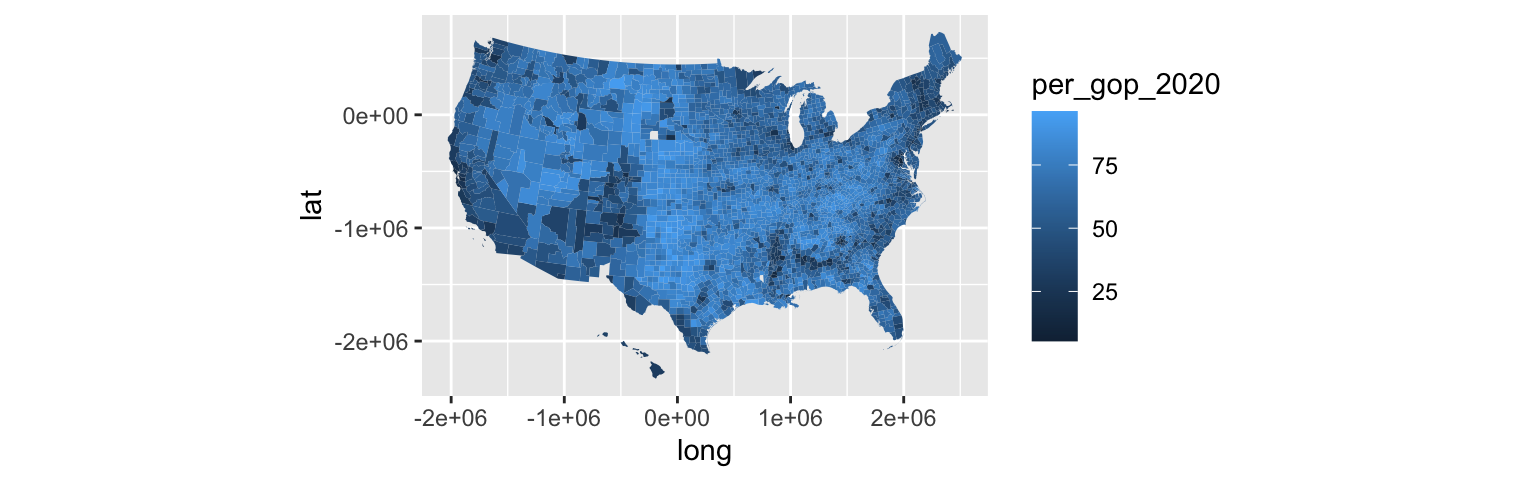


ggplot(mapping_data, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA) + 
  scale_fill_gradientn(colours = c("blue", "purple", "red"))


mn <- mapping_data %>% 
  filter(state_name == "Minnesota")
ggplot(mn, aes(x = long, y = lat, fill = per_gop_2020, group = group)) + 
  coord_equal() + 
  geom_polygon(color = NA) + 
  scale_fill_gradientn(colours = c("blue", "purple", "red"), values = scales::rescale(seq(0, 100, by = 10)))