About

BAYES IS HAVING A (LONG) MOMENT

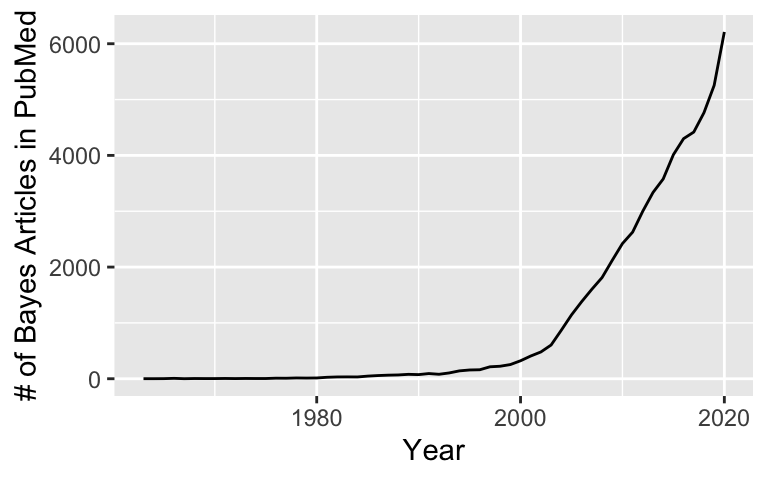
(Almost) all other STAT / MATH / ECON / BIO / PSYCH / ETC courses at Mac incorporate frequentist approaches to data analysis. This semester, we’ll study the increasingly popular Bayesian approach to statistics. So popular it’s popping up on TV shows (eg: The Big Bang Theory, Numbers), popular news sites & blogs (eg: FiveThirtyEight, Variance Explained), and in research1:



BUT IT’S OLD

But Bayesian statistics adheres to an old philosophy named for Reverend Thomas Bayes (1701-1761)2, hence the capital B Bayesian.



SO WHY NOW?

  1. Advances in computing.
    The sophisticated computing techniques required for Bayesian applications weren’t broadly available until the 1990s.


  1. Departure from tradition.

  2. Reevaluation of “subjectivity”
    Modern statistical practice is a child of the Enlightenment. A reflection of the Enlightenment ideals, frequentist methods were embraced as the superior, objective alternative to the broken, subjective Bayesian philosophy. Famous victims of this stigma include Alan Turing and Marilyn vos Savant who used Bayesian methods to crack the Enigma code and solve the Monty Hall problem, respectively.3

    This subjective stigma has slowly faded for several reasons.

    • All statistical analyses, whether frequentist or Bayesian, are subjective. Our incoming experiences and knowledge naturally inform what we measure, why we measure it, and how we model it.
    • Post-Enlightenment, “subjective” is no longer such a dirty word. After all, just as two bakers might use two different recipes to produce equally tasty bagels, two analysts might use two different techniques to produce equally informative analyses.
    • The Bayesian philosophy has been reevaluated as a natural approach to scientific inquiry. Recently, the Center for Mind, Brain and Consciousness at New York University even held a conference to debate the question “Is the brain Bayesian?”.



LET’S JOIN THE CONVERSATION!

  1. https://pubmed.ncbi.nlm.nih.gov/?term=bayesian&filter=years.1963-2020↩︎

  2. photo: https://en.wikipedia.org/wiki/Thomas_Bayes↩︎

  3. McGrayne, S. (2012). The theory that would not die - How Bayes’ Rule cracked the Enigma code, hunted down Russian submarines and emerged triumphant from two centuries of controversy. Yale University Press.↩︎