7 Combinatorial probability



RECOMMENDED READING

B & H Chapters 1.3 - 1.5.





7.1 Discussion


Motivating Example

  • An urn contains 3 marbles, numbered 1–3. If we pick 2 marbles with replacement, there are 9 possible outcomes: \[\{\color{red}{11}, 12, 13, 21, \color{red}{22}, 23, 31, 32, \color{red}{33}\}\] What’s the probability that we get 2 of a kind?

    Answer: \(3/9\)


  • An urn contains 100 marbles, numbered 1–100. If we pick 2 with replacement, what’s the probability we get 2 of a kind?

    Answer: There are too many possibilities to count by hand. Use combinatorics!









Calculating combinatorial probabilities

Suppose there are \(n\) equally likely outcomes in sample space \(S\) and \(m\) equally likely outcomes in event \(A \subseteq S\). Then \[P(A) = \frac{|A|}{|S|} = \frac{m}{n}\]









COUNTING METHODS

Method Ordered? Repetition? Counting
Multiplication Rule
# of ways to perform \(A_1,...,A_k\) if each \(A_i\) has \(n_i\) ways		 Yes Yes \(n_1 \cdot n_2 \cdots n_k\)
Permutations (distinct)
# of ways to permute (create a sequence using) \(k\) of \(n\) distinct objects		 Yes No \(\frac{n!}{(n-k)!} = n\cdot (n-1)\cdots (n-k+1)\)
Permutations (non-distinct)
# of ways to permute \(n\) non-distinct objects: there are \(r\) types of objects with sample sizes \(\sum_{i=1}^rn_i = n\)		 Yes No \(\frac{n!}{n_1!n_2!\cdots n_r!}\)
Combinations
# of ways to sample \(k\) of \(n\) distinct objects		 No No \(\left(\begin{array}{c} n \\ k \end{array}\right) = \frac{n!}{k!(n-k)!}\)











EXAMPLE 1

  1. Mac is 1 of 13 colleges in the MIAC. If all 13 schools compete in a baseball tournament:
    • How many ways can the teams come in 1st through 13th place?
    • How many ways can the teams come in 1st, 2nd, and 3rd place?
  2. A Minnesota license plate is a combination of 3 letters (A–Z) and 3 numbers (0–9).
    • How many unique license plates are possible?
    • How many unique license plates are possible if no letters or numbers are repeated?
  3. Let’s write some new “words”. Note: We’ll need to use permutations for non-distinct objects, a topic not on the video for today.
    • How many 3-letter words can we create using the letters in HEY?
    • How many 3-letter words can we create using the letters in HAH?
    • How many 13-letter “words” can we create using the letters in MATHEMAGICIAN?

  4. How many ways can we deal a poker hand (5 cards) using a standard deck (52 cards)?

  5. There are 26 students in a room. 13 are AMS majors and 13 are COMP majors. Suppose the students are randomly organized into a line.
    • What’s the probability that the students line up in alphabetical order?
    • What’s the probability that the AMS majors line up before the COMP majors? (AAAAAAAAAAAAACCCCCCCCCCCCC)





















7.2 Exercises

The following combinatorial probability exercises are all challenging. Work with your group to identify which counting rules would be useful and be patient. If you’re really excited about this material, you should take Combinatorics – a whole semester on counting!


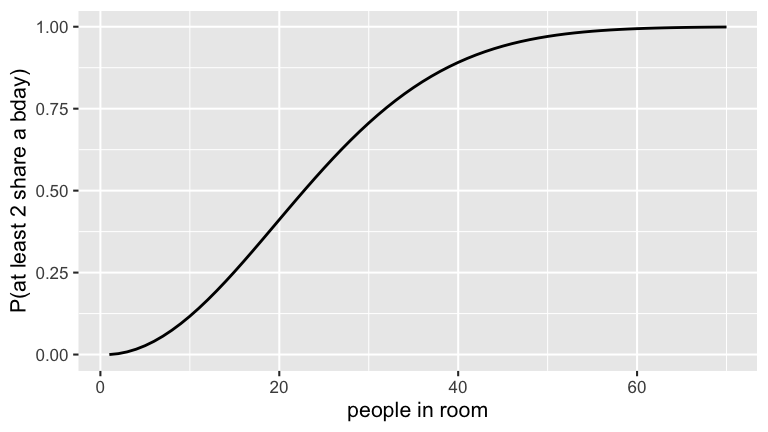
  1. The Birthday Problem
    Take a look at how many people are in this room. What’s the chance that at least 2 of us share a birthday? Is it closer to 0.01, 0.20, 0.50, 0.70, or 0.99? This is yet another famously puzzling question!

    You’ll solve this puzzle below.

    1. There are 23 people in a room. What’s the probability at least 2 of these 23 share the same birthday? What simplifying assumptions are you making in this calculation? Try the problem before looking at the following HINTS:
      • How many birthday combinations can there be?
      • In how many of these combinations are the birthdays unique (ie. nobody shares their birthday glory)?
      • What’s the complement of “at least 2 share”?


    1. Suppose there are \(n\) people in the room. Come up with a general formula to calculate the probability that at least 2 of \(n\) people share a birthday.
    2. How many people \(n\) would we need in the room for there to be at least a 99% chance that at least two share a birthday?
    3. Explain why the probability is higher than what we might initially expect.


    Check out a plot


  1. CHALLENGE
    A standard 52 card deck has 4 suits (see the rows below) and 13 ranks within each suit (see the columns below):

    If a 5 card hand is dealt from the deck, what’s the probability of getting…
    1. one pair (ie. 2 cards of the same rank)?
    2. two pairs?
    3. three of a kind (ie. 3 cards of the same rank)?
    4. a straight? (5 cards of sequential rank, not all the same suit)
    5. a flush? (5 cards of the same suit, any rank)
    6. a full house? (one pair and three of a kind)



  1. Extra Practice (Example 1.4.19 from Blitzstein & Hwang)
    Samuel Pepys, a gambling enthusiast, asked Isaac Newton which of the following events is most probable:
    • \(A\) = get at least one 6 in 6 dice rolls
    • \(B\) = get at least two 6s in 12 dice rolls
    • \(C\) = get at least three 6s in 18 dice rolls
    Help them out!


  1. Extra: From Homework
    An apartment building has eight floors. Suppose 4 people get on the elevator on the first floor and travel to one of the 7 higher floors (floors 2 – 8). Assume they’re equally equally likely to get off on any of the 7 floors.
    1. How many ways can the riders get off on their floors?
    2. How many ways can the riders get off on different floors?
    3. What is the probability they all get off on different floors?
    4. What is the probability they all get off on the same floor?