1 Foundations of probability



READING:

For more on this topic: B & H Chapters 1.1 - 1.3, 1.6 - 1.7








1.1 Discussion

In this short video, mathemagician Dr. Arthur Benjamin makes a compelling plea to replace calculus with probability (& statistics) at the top of the math curriculum pyramid. Why? We live in a world of randomness, uncertainty, and risk, thus probability has myriad applications in our everyday lives.

Probability is the logic of uncertainty - it provides a mathematical framework that allows us to:

  • formalize uncertainty;
  • make informed decisions about uncertain events;
  • draw inferences using data arising from uncertain processes; and
  • better understand the world around us.










The need for Probability

Without the formalism that Probability provides, humans are notoriously bad at assessing uncertainty. Why?


Evolution.  We evolved to avoid certain mistakes at the cost of making others. Example: It’s pitch black & you hear a thud. P(it’s a burglar) vs P(it’s your roommate).
Emotion.  Uncertainty is assessed by the same parts of the brain that handle our emotions (the dopaminergic system and amygdala). Example: P(keeping her cat in her lap will result in my sister’s team’s win) \(\approx\) 1.
Brain Structure.  The two hemispheres of the brain can come to different conclusions and battle it out to see which will dominate.





















1.2 Exercises

Goals

The following exercises will introduce the fundamentals of studying uncertainty.



Getting Started

Put a mark in the table on the board according to your major and the initial of your last name. Summarize this table below:

A-M N-T U-Z Total
AMS
not AMS
Total 1



1.2.1 Set theory foundations

Suppose we select a student at random. Before we can quantify the inherent randomness in this “experiment”, we must understand its possible outcomes. To this end, consider some general definitions:

  • Sample space “\(S\)” is the collection of all possible outcomes of an experiment.
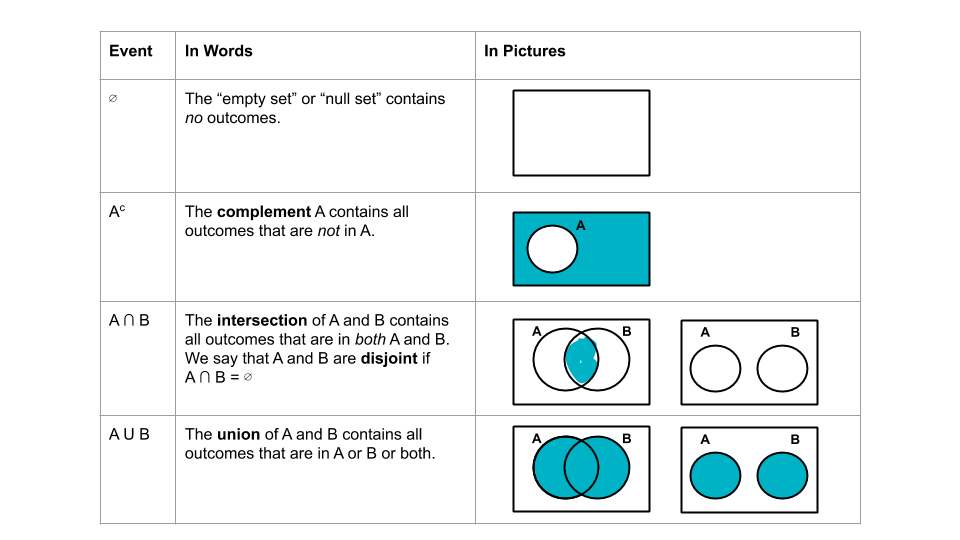
  • An event is an element or collection of elements in the sample space, typically denoted by capital letters (eg: A, B, C). Thus an event is a subset of the sample space S - all outcomes in A are also in S: \[A \subseteq S\]

In our experiment, sample space \(S\) is the collection of all students in this room. Some events of interest are:

  • \(A\) = the student is an AMS major
  • \(B\) = the student’s initial is A-M
  • \(C\) = the student’s initial is N-T
  • \(D\) = the student’s initial is U-Z



Special events



  1. Group event
    1. Introduce yourself to your group (eg: name, pgp, major). Share the most “random” thing that you experienced today or over winter break.
    2. Define a new event \(E\) to which all of your group members belong. You’ll share this with the class. Bonus points if nobody outside your group belongs to \(E\), ie. if it’s really “random”.



  1. Class set theory
    Suppose we select a student at random. For each possible event below, specify the correct notation: \(A^c\), \(B^c\), \(A \cap B\), \(A \cup B\)
    1. the person is an AMS major or their name starts with A-M (or both)
    2. the person is an AMS major whose name starts with A-M
    3. the person’s last name doesn’t start with A-M



  1. DeMorgan’s Law: Neither / Nor
    For each event below, describe the event in words and represent it on a Venn diagram.
    1. \((A \cup B)^c\) is the group consisting of…
    2. \(A^c \cap B^c\) is the group consisting of…
    3. How do \((A \cup B)^c\) and \(A^c \cap B^c\) compare? This property, one of DeMorgan’s Laws, holds in general. Translate this property into words.



  1. DeMorgan’s Law: Either / Or
    For each event below, describe the event in words and represent it on a Venn diagram.
    1. \((A \cap B)^c\) is the group consisting of…
    2. \(A^c \cup B^c\) is the group consisting of…
    3. How do \((A \cap B)^c\) and \(A^c \cup B^c\) compare? This property, one of DeMorgan’s Laws, holds in general. Translate this property into words.



1.2.2 Probability foundations

Now that we better understand the possible outcomes of our experiment, let’s explore the uncertainty involved.



INFORMAL definition

Informally, probability is a measure of uncertainty, taking values between 0 (impossible) & 1 (almost sure). There are a couple of ways to interpret probabilities:

  • frequentist interpretation: long-run relative frequency of an event
  • Bayesian interpretation: relative plausibility of an event



EXAMPLE

Suppose we flip a fair coin. Then the probability of Heads is 0.5. Which of the following interpretations makes sense to you? Which is frequentist / Bayesian?

  1. If we flip the coin over and over and over, we’ll get Heads roughly 50% of the time
  2. Heads and Tails are equally plausible
  3. Both interpretations make sense.

A meteorologist says there’s a 99% chance of snow today. Which of the following interpretations makes sense to you? Which is frequentist / Bayesian?

  1. If we observe hypothetical todays over and over and over, it’ll snow on roughly 99% of todays
  2. This calculation is wrong. It will either snow or not snow, thus the probability must be 0 or 1.
  3. Snow is almost certain
  4. Both interpretations make sense.





FORMAL definition (from Blitzstein & Hwang)
A probability function \(P\) takes an event \(A \subseteq S\) as input and returns \(P(A)\), a real number between 0 and 1, as output. The function \(P\) must satisfy the following axioms:

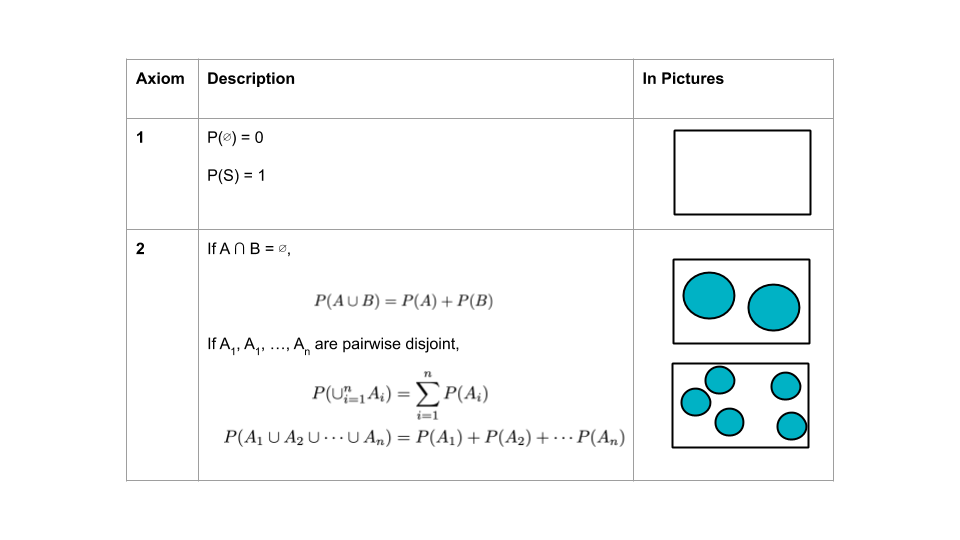
  1. Apply the probability axioms
    1. What’s the probability that the selected person is a student in this room?
    2. What’s the probability that the person’s last name starts with A-M or N-T? Think: are these events disjoint?



  1. Intuiting the properties of probability
    Many properties fall from the two probability axioms. Let’s try to intuit these before examining their formal definitions. Drawing Venn diagrams might help!
    1. Calculate \(P(B^c)\), the probability that the student’s last name doesn’t start with A-M.
    2. Let \(E\) be the event that the student’s last name starts with A-G. How does \(P(E)\) compare to \(P(B)\): \(P(B) = P(E)\), \(P(B) \le P(E)\), \(P(B) \ge P(E)\)
    3. Calculate \(P(A \cup B)\), the probability that the student is either an AMS major or their last name starts with A-M (or both).



  1. Properties of probability
    From the two probability axioms, we can establish the following properties of probability. Redo the previous exercise using these properties. Were you right?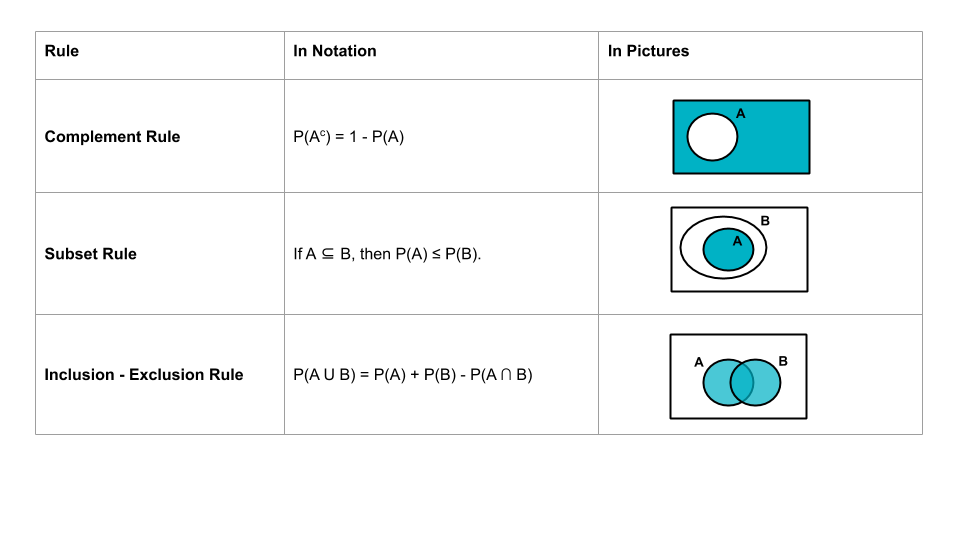

  2. Apply the probability properties
    Try another example. Fake news is making news.

    According to buzzfeed data (an apt source for this example), among U.S. voters:

    • 48% voted for Hillary Clinton (rounded for white board friendliness)
    • 58% believed the above headline
    • 22% are Clinton voters that believed the headline

    Randomly select one adult voter. Let \(A\) be the event that they voted for Clinton and \(B\) be the event that they believed the headline.

    1. Restate the 48%, 58%, and 22% figures using probability notation (eg: \(P(A \cup B\))).
    2. Utilizing careful notation and stating the relevant probability axiom / property, calculate the probability that the person…
      • didn’t vote for Clinton
      • either voted for Clinton or believed the headline
      • is a Clinton voter that didn’t believe the headline
      • is neither a Clinton voter nor a headline believer?

    3. Contingency tables can also help us build intuition. Fill in the missing cells and, once you do, utilize the table to confirm your answers to part b.

      \(B\) \(B^c\) Total
      \(A\) 0.48
      \(A^c\)
      Total 0.58 1



    Solutions

    1. \(P(A) = 0.48\), \(P(B) = 0.58\), \(P(A \cap B) = 0.22\)
    2. .
      • \(P(A^c) = 1 - P(A) = 1 - 0.48 = 0.52\)
      • \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = 0.48 + 0.58 - 0.22 = 0.84\)
      • \(A = (A \cap B) \cup (A \cap B^c)\) where \((A \cap B)\) and \((A \cap B^c)\) are disjoint
        \(P(A) = P(A \cap B) + P(A \cap B^c)\)
        \(P(A \cap B^c) = P(A) - P(A \cap B) = 0.48 - 0.22 = 0.26\)
      • \(P(A^c \cap B^c) = P((A \cup B)^c) = 1 - P(A \cup B) = 1 - 0.84 = 0.16\)

    3. .

      \(B\) \(B^c\) Total
      \(A\) 0.22 0.26 0.48
      \(A^c\) 0.36 0.16 0.52
      Total 0.58 0.42 1



  1. Practicing good habits
    Incorrect notation leads to incorrect statements. For example, flip a coin & let \(A\) be the event that you get Heads and \(B\) be the event that you get Tails. The probability of getting either Heads or Tails is, of course, 1. Indicate which of the following summaries of this statement is both correct & complete. For the others, specify why the proof is incorrect or incomplete.

    1. \(P(A \cup B) = 1\)
    2. \(A + B = 1\)
    3. \(P(A) \cup P(B) = 1\)
    4. 1



  1. Challenge: prove the properties of probability
    We can prove the properties of probability using only the probability axioms. Drawing Venn diagrams will aid our intuition.

    1. Prove the complement rule. HINT: What’s the union of \(A\) and \(A^c\)?
    2. Prove the subset rule. HINT: How can we write \(B\) as the union of \(A\) and another event?
    3. Prove the inclusion-exclusion rule. HINT: Think about the other hints.



  1. Optional extra practice (solutions online)
    A poll aggregator wants to combine the results of 2 different pollsters into 1 single prediction. In doing so, they take into account the track record for the 2 pollsters.

    • In 30% of past elections, pollster 1’s predictions were “right” (results were within the margin of error of their prediction).
    • In 5%, both pollsters were right.
    • In 10%, pollster 1 was wrong but pollster 2 was right.

    For the next election, let \(A\) be the event that pollster 1 is right and \(B\) be the event that pollster 2 is right.

    1. Write down all of the information you are given about \(A\) and \(B\) in the problem.
    2. What’s the probability that pollster 2 is right?
    3. What’s the probability that at least 1 of the 2 pollsters is right?
    4. What’s the probability that at least 1 is wrong?
    5. Fill out a contingency table and utilize this to confirm your answers above.


    Solutions

    1. 0.3 = \(P(A)\)
      0.05 = \(P(A \cap B)\)
      0.10 = \(P(A^c \cap B)\)

    2. \(P(B) = P(A \cap B) + P(A^c \cap B) = 0.15\)

    3. \(P(A \cup B) = 0.3 + 0.15 - 0.05 = 0.40\)

    4. \(P(A^c \cup B^c) = P((A \cap B)^c) = 1 - P(A \cap B) = 0.95\)

    5. .

      \(B\) \(B^c\) Total
      \(A\) 0.05 0.25 0.30
      \(A^c\) 0.10 0.60 0.70
      Total 0.15 0.85 1