2 Conditional probability
GETTING STARTED
- Homework 1 & Checkpoint 1
- syllabus pages 1-3
- activity 1, exercise 9
RECOMMENDED READING
B & H Chapter 2.1 & 2.2.
Where are we?
2.1 Discussion
Conditional Probability
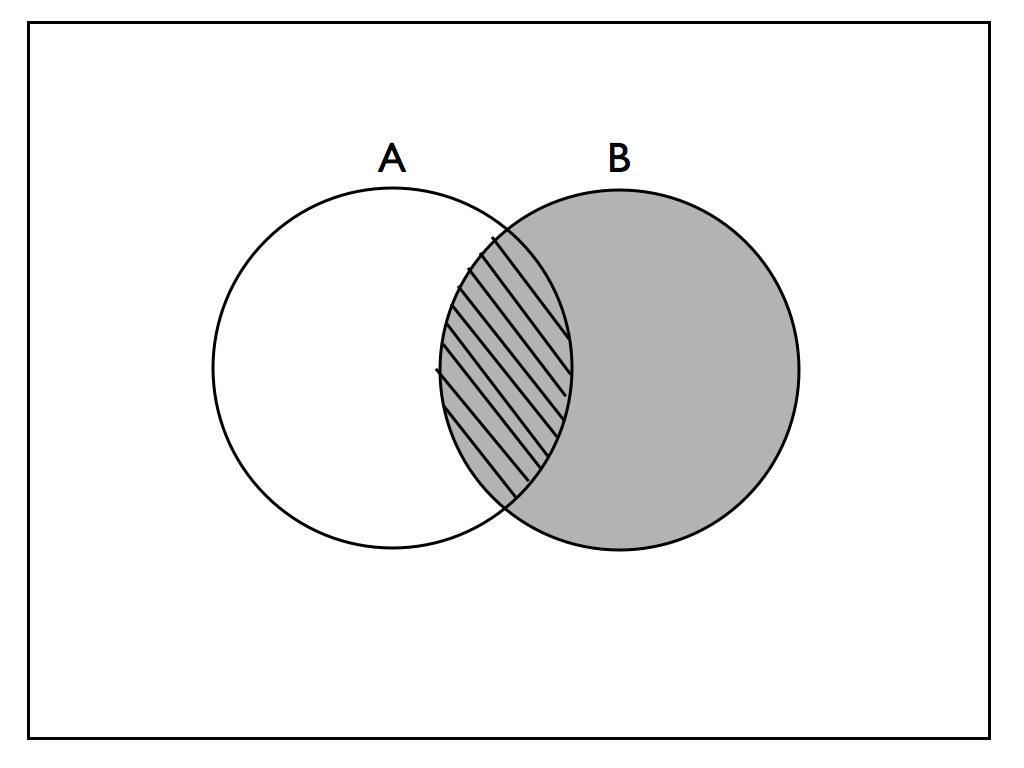
The conditional probability of “\(A\) given \(B\)” is the probability \(A\) occurs given the information \(B\) occurs: \[P(A|B) = \frac{P(A\cap B)}{P(B)}\]
Similarly, the conditional probability \(B\) occurs given the information \(A\) occurs is \[P(B|A) = \frac{P(A\cap B)}{P(A)}\]
Calculating \(P(A \cap B)\)
We can rearrange the conditional probability to calculate the joint probability of \(A\) and \(B\): \[P(A \cap B) = P(A|B)P(B)\]
EXAMPLE 1
Order each pair of probabilities below.1
\(A\) = the person next to you is hungry
\(B\) = the person next to skipped breakfast\[P(A) \underline{\hspace{1in}} P(A|B)\]
\(A\) = the person next to you owns a pair of skis
\(B\) = the person next to has no idea how to ski\[P(A) \underline{\hspace{1in}} P(A|B)\]
\(A\) = your friend’s car is on fire
\(B\) = there’s something wrong with your friend’s car.\[P(A|B) \underline{\hspace{1in}} P(B|A)\]
EXAMPLE 2
A fivethirtyeight.com article, Comic Books Are Still Made By Men, For Men And About Men examines features of DC & Marvel characters. An examination of nearly 7000 of these characters (from the raw data) demonstrates the following DC & Marvel stereotypes, represented in a contingency table here.
- Pick a character at random. What’s the probability it’s “good”?
- Suppose the character has red eyes. What’s the probability it’s “good”?
EXAMPLE 3
After ~46% of voters voted for Trump in the 2016 election, CNN provided insight with some exit poll data. NOTE: This isn’t a contingency table!
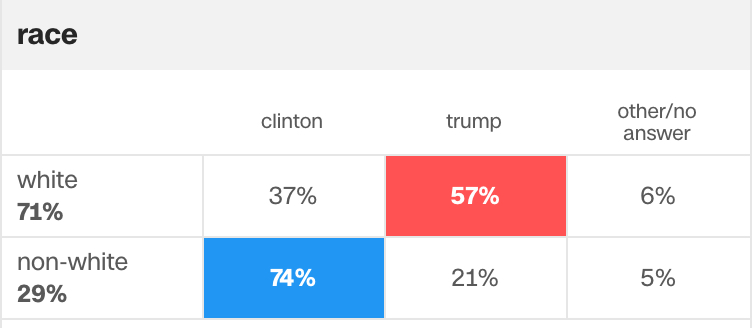
- Summarize the “57%” & “71%” statistics using probability notation.
- What proportion of 2016 voters were white Trump supporters?
2.2 Exercises
On the first day of class, we talked about how humans are notoriously bad at assessing uncertainty. In these exercises you’ll explore a classic example that counters most people’s intuition: A new friend tells you that they have 2 children. To greatly oversimplify things, we’ll assume binary gender identities for both children: boy or girl. Thus sample space \(S\) captures the 4 possibilities:
\[S = \{bb, bg, gb, gg\}\]
NOTE: Birth order matters. Thus event \(bg\) (first child is \(b\) and second is \(g\)) is different than event \(gb\) (first child is \(g\) and second is \(b\)). Finally, define the following events:
- \(A\) = both children are boys
- \(B\) = at least one child is a boy
- \(C\) = at least one child is a boy that was born in the morning
- \(D\) = the eldest child is a boy that was born in the morning
- \(E\) = at least one child is a boy that was born in the morning during the first half of the year
GUT CHECK
Our main question is whether both children are boys (\(A\)). Without any information about the children, the probability of this event is \[P(A)\]
Suppose we were to learn some information about the children through conversation (\(B\) or \(C\)). How, if at all, does this information change our understanding of \(A\). Specifically, how do \(P(A)\), \(P(A|B)\), and \(P(A|C)\) compare? (Just go with your gut, don’t do any calculations.)\(P(A) = P(A|B) = P(A|C)\)
\(B\) and \(C\) don’t tell us anything about \(A\).\(P(A) < P(A|B) = P(A|C)\)
\(B\) increases the chance of \(A\). But the added info about time of day (\(C\)) doesn’t change the calculation.\(P(A) < P(A|B) < P(A|C)\)
\(B\) increases the chance of \(A\). \(C\) increases the chances even more!
Defining assumptions
In order to calculate the probabilities above, we have to make some assumptions. For each pair of events below, specify the most simple yet realistic assumptions we can make. Comment on how these might oversimplify reality.- \(P(B)\) vs \(P(G)\)
- \(P(\text{morning})\) vs \(P(\text{evening})\)
- \(P(\text{first half of year})\) vs \(P(\text{second half of year})\)
- \(P(B)\) vs \(P(G)\)
- At least one boy
- Calculate \(P(A)\).
- You learn through conversation that at least one child is a boy (\(B\)). Calculate \(P(A|B)\).
- Calculate \(P(A)\).
- Time of day
Next, let’s incorporate birth time of day.Write out a new sample space that specifies every possible combination of gender identity (\(b\) or \(g\)) and birth time of day for the 2 children. For consistency, record time of day as \(m\) (morning) or \(n\) (night). Two rows are given to you as an example.
gender: child 1 time of day: child 1 gender: child 2 time of day: child 2 \(b\) \(m\) \(b\) \(m\) \(b\) \(m\) \(b\) \(n\) - You learn through conversation that at least one child is a boy born in the morning. Calculate \(P(A|C)\) using the sample space you created above (we can take a more rigorous approach after we discuss “independence” next week).
- You learn through conversation that the first born is a boy born in the morning. Calculate \(P(A|D)\).
Whoa. Are you surprised?!? Provide an intuitive explanation for why \(P(A|B) < P(A|C) < P(A|D)\).
- Extra practice (to complete outside class)
You learn through conversation that at least one child is a boy born in the morning during the first half of the year. Calculate \(P(A|E)\) and explain why it makes sense that \(P(A|E) > P(A|C)\).
- Optional extra practice (solutions online)
We roll two fair six-sided dice. Each one of the 36 possible outcomes is assumed to be equally likely.- Find the probability that doubles are rolled.
- Given that the roll results in a sum of 4 or less, find the conditional probability that doubles are rolled.
- Find the probability that at least one die roll is a 6.
- Given that the two dice land on different numbers, find the conditional probability that at least one die roll is a 6.
- Given that the minimum of the two rolls is equal to 3, what is the probability that the maximum of the two rolls is equal to 4?
Solution
Let- \(A\) = doubles = \(\{11, 22, 33, 44, 55, 66\}\)
\(P(A) = 6/36 = 1/6\)
- \(B\) = sum of 4 or less = \(\{11,12,21,13,31,22\}\)
\(A \cap B\) = \(\{11,22\}\)
\(P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{2/36}{6/36} = \frac{1}{3}\)
- \(C\) = at least one 6 = \(\{16, 61, 26, 62, 36, 63, 46, 64, 56, 65, 66\}\)
\(P(C) = 11/36\) - \(D\) = \(A^c\)
\(C \cap D = \{16, 61, 26, 62, 36, 63, 46, 64, 56, 65\}\) \(P(C|D) = \frac{P(C \cap D)}{P(D)} = \frac{10/36}{1 - 6/36} = \frac{1}{3}\)
- \(F\) = minimum is 3 = \(\{33,34,43,35,53,36,63\}\)
\(E \cap F = \{34,43\}\)
\(P(E|F) = \frac{P(E \cap F)}{P(F)} = \frac{2/36}{7/36} = \frac{2}{7}\)
- Find the probability that doubles are rolled.
- Hot tip
Re-organizing your notes after class is a good way to review the material while making your work easier to reference in the future. You’re encouraged to reorganize your notes after every class.
The last example is from Mine Cetinkaya Rundel.↩