8 Discrete RVs: Binomial & Poisson
READING
For more on this topic, read B & H Chapter 3.1 - 3.3.
8.1 Discussion
Probability Models for Discrete RVs
A probability mass function (pmf) \(p_X(x)\) describes the plausible values of discrete RV \(X\) and their relative likelihood. A valid pmf satisfies
- \(0 \le p_X(x) \le 1\)
- \(\sum_{\text{all }x} p_X(x) = 1\)
Using \(p_X(x)\):
- We can interpret the pmf as a probability: \(p_X(x) = P(X=x)\)
- For some set \(A\), \(P(X \in A) = \sum_{x \in A} p_X(x)\)
Detail: \(X\) vs \(x\)
\(X\) is a label for the random variable. \(x\) is the value of \(X\) that we observe.
EXAMPLE
Each time they host a dinner party, your friend A randomly seats you and 4 of your other friends (6 people total) at one side of a table. Let \(X\) be the number of people seated between you and A.
- Represent the pmf of \(X\), \(p_X(x)\), in table format.
- Define a formula for this pmf.
- Sketch & describe \(p_X(x)\).
- You’d prefer to have at least 2 friends between you and A. What are the chances?
Named Probability Models
The probability model in the example above is very context specific. However, there exist named probability models (or “distributions”) that can be tuned to appropriately model large groups of random variables that have similiar frameworks. You’ll explore two discrete models today: the Binomial and Poisson.
NOTE: We will explore multiple named models throughout the semester. These will be summarized in the appendix of the online course manual. You’re also encouraged to make an appendix of your own!
8.2 Exercises
8.2.1 Binomial
Counting Voters
Political polls strive to reflect voter sentiment. Consider polling just 4 constituents (trials) about senator Bernie Sanders (Vermont). They either approve of Sanders (success \(S\)) or disapprove (failure \(F\)). Of course, the results can vary from poll to poll, depending upon which constituents are contacted. For example, in one possible poll, the first 3 people might approve and the last disapproves: \(SSSF\). Using combinatorial tools, summarize the number of ways to get 0, 1, 2, 3, or 4 successes in these 4 trials.
Successes Number of ways 0 1 2 3 4 Total 16
NOTE: Pascal’s triangle is constructed from binomial coefficients: \[\left(\begin{array}{c} n \\ k \end{array} \right) = (k+1)^{\text{st}} \text{ entry in the } (n+1)^{\text{st}} \text{ row}\] Use Pascal’s triangle to confirm the entries in your table.

Bernie Sanders: 4 trials
Sanders has the highest approval rating (success rate) in the senate at more than 60%. Independently poll 4 constituents and let \(U\) be the number that approve of Sanders. Thus \(U\) is a discrete RV with pmf \(p_U(u) = P(U = u)\).Calculate \(p_U(1) = P(U = 1)\). HINTS:
- In how many ways can 1 of 4 voters approve?
- Keeping in mind that \(S/F\) aren’t equally likely, what’s the probability of any one of these 1-success sequences (eg: SFFF)?
- In how many ways can 1 of 4 voters approve?
- Summarize \(p_U(u)\) in a table.
Define a formula for \(p_U(u)\). Don’t forget to specify the support, ie. the values \(u\) for which \(p_U()\) is defined.
Bernie Sanders: 20 trials
Next, suppose we poll 20 constituents. Let \(V\) be the number of these that approve of Sanders.- What values of \(V\) might we observe?
- Calculate \(p_V(10) = P(V = 10)\), the probability that exactly \(V = 10\) of 20 voters approve. (Revisit the hints from above.)
- Generalize your work from part b to construct a formula that, for any \(v \in \{0,1,...,20\}\), can be used to calculate \(p_V(v)\): \[p_V(v) = P(V=v)\]
- Mitch McConnell: 20 trials
Mitch McConnell (Kentucky) is one of the least popular senators with an approval rating less than 40%. Let \(W\) be the number of 20 polled constituents that approve of McConnell. Write out a general formula for \(p_W(w) = P(W=w)\).
The Binomial probability model
We can extend your work above to any sized poll about any politician. For a given politician, the number of polled constituents \(X\) that approve of their work depends upon two parameters:- \(n\) = a fixed number of independent trials (ie. polled constituents);
- \(p\) = probability of success in each trial (ie. underlying approval rating).
Any \(X\) that satisfies this structure has a Binomial model with parameters \(n\) and \(p\). In notation: \[X \sim Bin(n,p)\]
Derive a formula for the pmf of \(X\), \(p_X(x) = P(X=x)\) for \(x \in \{0,1,2,...,n\}\).
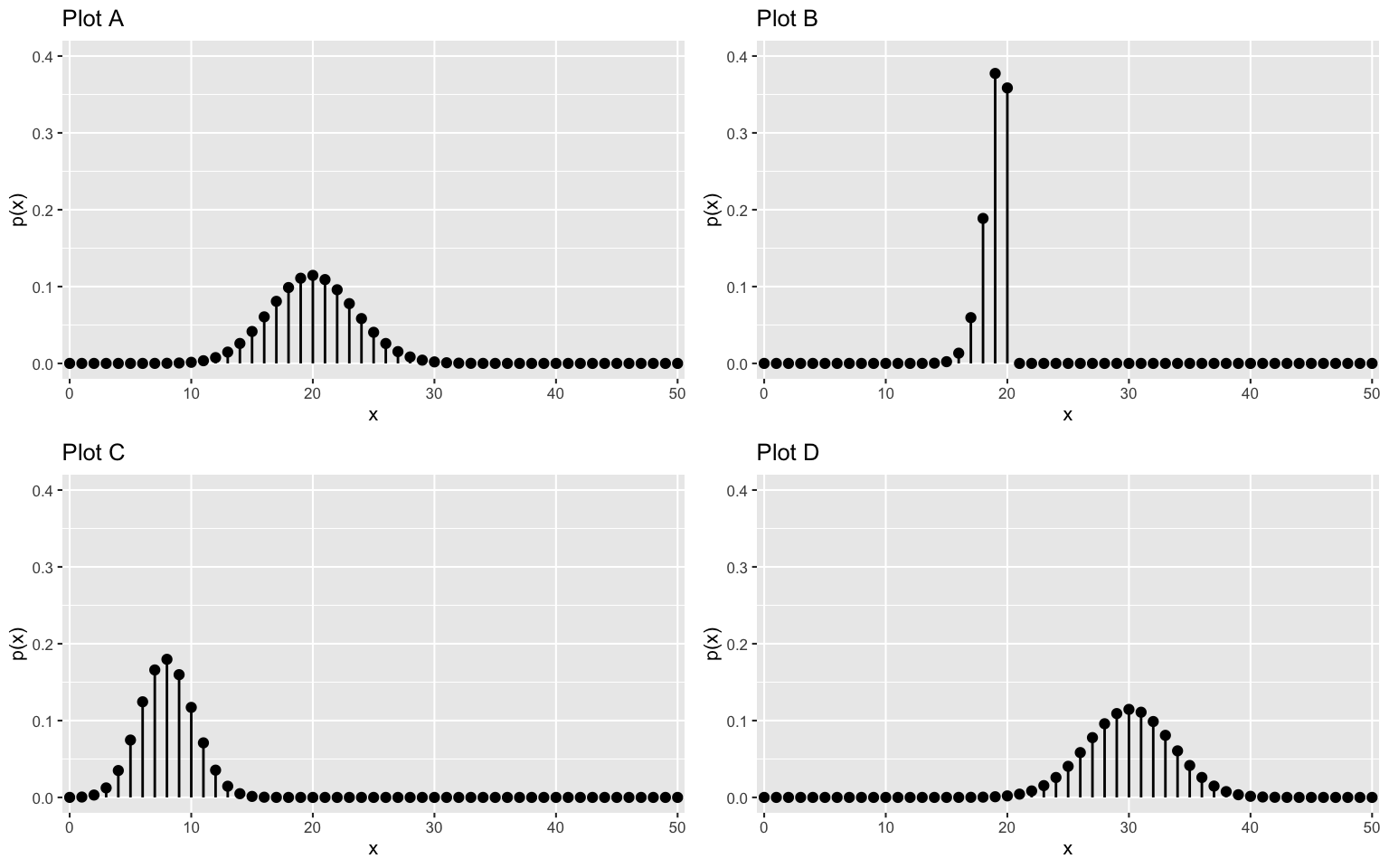
Match each pmf plot below to one of the following settings. Subsequently, use these pmfs to describe the behavior of the corresponding random variable.
\(n\) \(p\) Senator Plot 20 0.40 McConnell 20 0.95 Super Popular 50 0.60 Sanders 50 0.40 McConnell
Show that \(p_X(x)\) is a valid pmf. That is:
- \(p_X(x) \ge 0\); and
- \(\sum_{x=0}^{n} p_X(x) = 1\).
HINT: The Binomial Theorem guarantees that for any \(a,b \in \mathbb{R}\), \[(a+b)^n = \sum_{x=0}^n \left(\begin{array}{c} n \\ x \end{array}\right) a^xb^{n-x}\]
- \(p_X(x) \ge 0\); and
- \(n\) = a fixed number of independent trials (ie. polled constituents);
Binomial or not?
Not every RV is Binomial! For each scenario below, identify whether \(X\) is Binomial:- \(X\) has PMF \[p_X(x) = \left(\begin{array}{c} 10 \\ x \end{array} \right) 0.7^x 0.3^{10-x} \;\; \text{ for } x \in \{0,1,2,...,10\}\]
- \(X\) = the weight of a student’s backpack
- \(X\) = the number of 6s in one die roll
- \(X\) = the number of 6s in 9 dice rolls
- \(X\) = the number of die rolls until we get our first 6
- We randomly draw & eat 10 M&Ms from a bag. \(X\) = the number that are red
8.2.2 Poisson
The Poisson is used to model \(X\) under the following assumptions:
- \(X \in \{0,1,2,...\}\) is the number of times that an event occurs in a time interval; where
- events are assumed to occur at a rate of \(\lambda\) per time interval.
In this case,
\[X \sim \text{Pois}(\lambda)\]
with pmf
\[p_X(x) = \frac{e^{-\lambda}\lambda^x}{x!} \hspace{.25in} \text{ for } x\in\{0,1,2,...\}\]
Consider some Poisson applications:
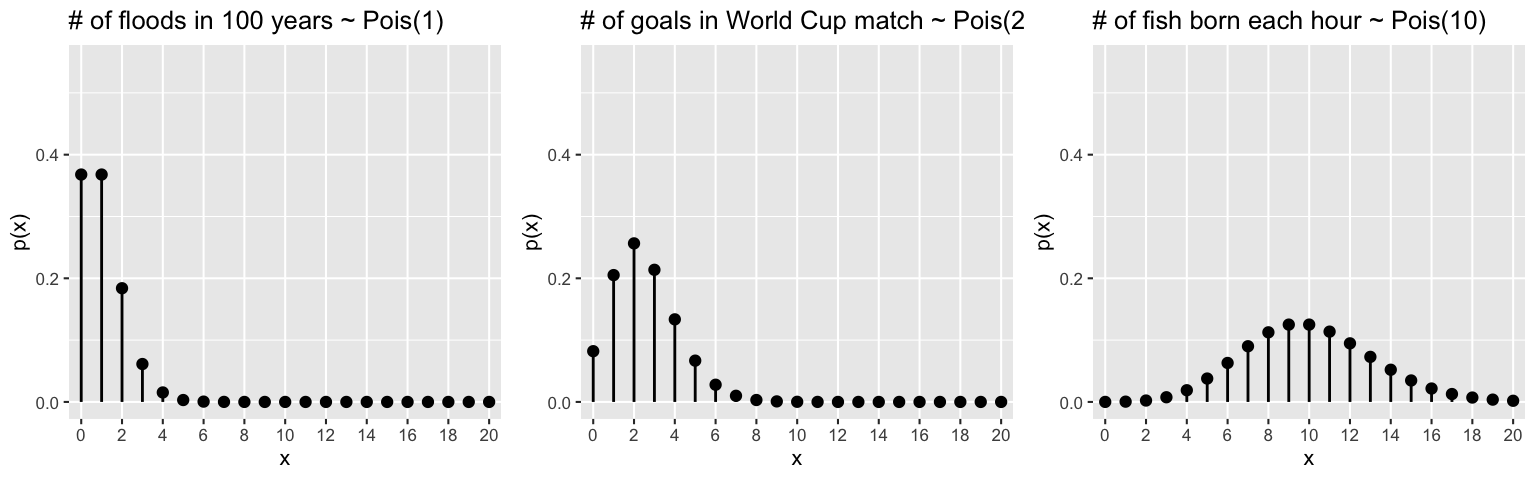
- Binomial vs Poisson
For each RV below, explain whether the Binomial or Poisson would be the more appropriate model.- \(X\) = number of puppies that walk through campus today
- \(X\) = number of the next 20 puppies walking through campus that are brown
- \(X\) = number of her next 5 matches that Serena Williams (a famous tennis player) wins
- \(X\) = number of aces (nice shots) that Serena Williams has in her next match
Poisson calculations
Let \(X\) be the number of cars that pass through the Snelling-Grand intersection each minute and suppose that \(X \sim \text{Pois}(20)\):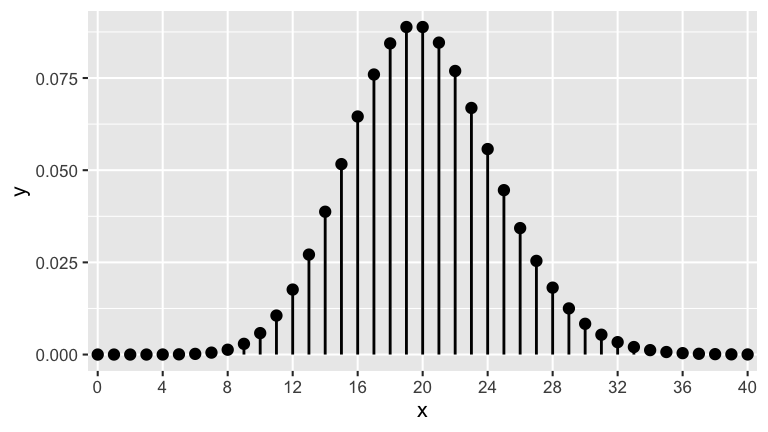
- What values can \(X\) take?
- Write out the formula for the pmf of \(X\).
- Calculate the probability that 17 cars pass in the next minute.
BONUS
Prove that the Pois(\(\lambda\)) pdf is valid. HINT: You’ll need to use the fact that, by definition,\[e^y = \sum_{k = 0}\frac{y^k}{k!}\]