5 Law of Total Probability & Bayes’ Rule
RECOMMENDED READING:
B & H Chapters 2.3 & 2.4.
5.1 Discussion
Motivating example
After leading the kneeling protests in the NFL, Nike signed Colin Kaepernick for a new ad campaign. image source

Yet Americans are split on the movement that Kaepernick represents (thus Nike’s move). According to a late 2017 CBS poll:
- 27% of Americans i.d. as liberal;
- 45% of Americans i.d. as moderate; and
- 28% of Americans i.d. as conservative.
Further, when asked “Do you approve or disapprove of football players protesting by kneeling during the national anthem?”
- 74% of liberals somewhat / strongly approved;
- 32% of moderates somewhat / strongly approved; and
- 16% of conservatives somewhat / strongly approved.
EXAMPLE 1: gut check
Answer the questions without any formal calculations. Think about what information you’re taking into account.
- Roughly what percentage of Americans approve of the kneeling protests: 20%, 30%, 40%, 50%, or 70%?
- Suppose you meet a new friend that indicates their support for the kneeling protests. Roughly what’s the chance that they’re conservative: 10%, 30%, or 50%?
EXAMPLE 2: set up a contingency table
- Summarize the given info using probability notation.
- Do liberals, moderates, & conservatives (as defined here) partition the sample space of all Americans?
- Fill in the following contingency table with this information.
| Politics | Approve (\(A\)) | Disapprove (\(A^c\)) | Total |
|---|---|---|---|
| Liberal (\(L\)) | |||
| Moderate (\(M\)) | |||
| Conservative (\(C\)) | |||
| Total | 1 |
EXAMPLE 3: utilize the contingency table
Utilize the contingency table to answer the questions below.
Pick a person at random. What’s the probability that they approve of players kneeling?
Prior to learning anything about this person, the chance that they’re conservative is \(P(C) = 0.28\). However, suppose the person tells you that they approve of kneeling. What’s the updated or posterior probability they’re conservative in light of this data? Explain why this is smaller than the prior probability.
Similarly, we can calculate the posterior probability that your new friend is a liberal or moderate. Comment on the shift of our understanding from the prior to the posterior.
party prior \(P(...)\) posterior \(P(...|A)\) \(L\) 0.27 \(M\) 0.45 \(C\) 0.28 Total 1 1
BONUS: A Sankey diagram which provides a visual summary of this information (more effectively than a Venn could!).
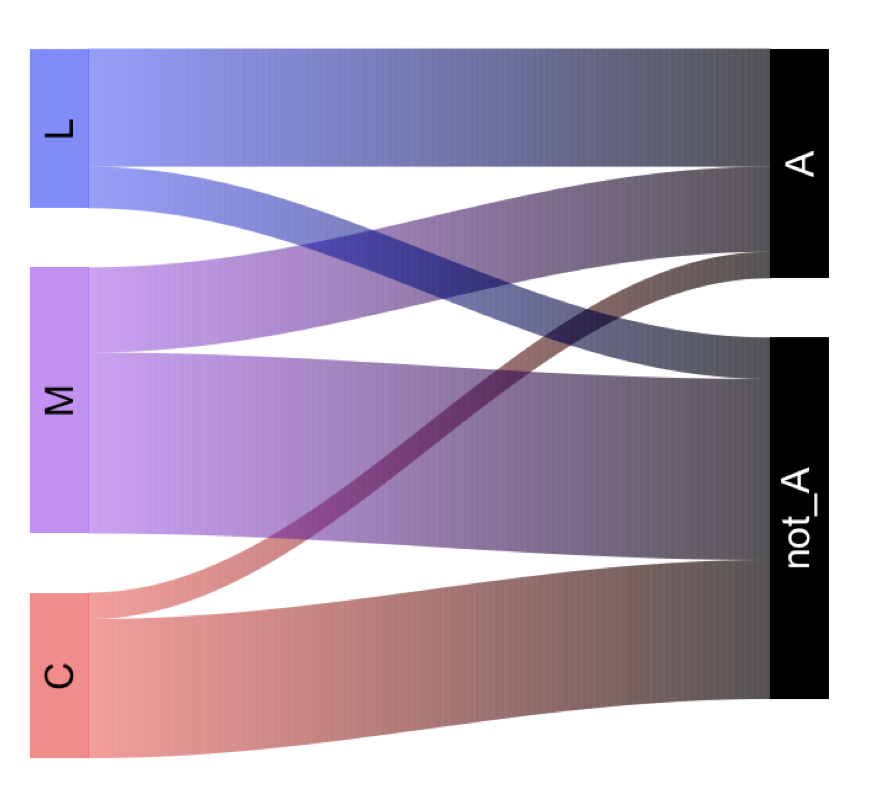
EXAMPLE 4: Law of Total Probability
In the previous example, you implemented the Law of Total Probability (LTP) to calculate \(P(A)\)…without calling it that. Give a rigorous mathematical proof of this result using probability notation and only the original given information (not the contingency table).
Law of Total Probability (LTP)
Suppose \(\{A_1, A_2, \ldots, A_k\}\) partition \(S\). Then for any event \(B \subseteq S\), \[B = \cup_{i=1}^k (B \cap A_i) = (B \cap A_1) \cup (B \cap A_2) \cup \cdots \cup (B \cap A_k)\] It follows that \[P(B) = \sum_{i=1}^k P(B \cap A_i) = \sum_{i=1}^k P(B | A_i)P(A_i) \;.\]
Special case: for the simple partition \(\{A,A^c\}\), \[P(B) = P(B \cap A) + P(B \cap A^c) = P(B | A)P(A) + P(B | A^c)P(A^c) \;.\]
What’s the use? LTP is useful when we want to know the unconditional \(P(B)\), but only have info about the conditional pieces \(P(B|A_i)\). We can combine these pieces to get the whole.
EXAMPLE 5: Bayes’ Rule
In the previous example, you also implemented Bayes’ Rule to calculate \(P(C|A)\)…without calling it that. Give a rigorous mathematical proof (using probability notation) of this result.
Bayes’ Rule
\[P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{P(B|A)P(A)}{P(B)}\]
Thus the posterior probability of \(A\) in light of information \(B\) (\(P(A|B)\)) is influenced by:
- the prior probability of \(A\) (\(P(A)\))
- the chances of observing data \(B\) if \(A\) occurs (\(P(B|A)\))
- the overall chance of observing \(B\) (\(P(B)\))
What’s the Use? Bayes’ Rule is useful when we want to know the conditional \(P(A|B)\), but only have info about the reverse conditional \(P(B|A)\).
Notable: “Bayes’ Rule”, named for Reverend Thomas Bayes (1702–1761), is the foundational philosophy of Bayesian statistics. As we’ll discuss, there’s historical controversy surrounding Bayes’ Rule!
5.2 Exercises
Practice (with solution online)
Edward Snowden leaked documents from the NSA’s PRISM surveillance program. PRISM uses an algorithm to flag communications that are potentially “terroristic” in nature. How effective is PRISM’s algorithm? Let’s make the following assumptions:- 1/1,000,000 communications (eg: calls, emails) are terroristic
- PRISM has a 1% false negative rate
(1% of terroristic communications are not flagged) - PRISM has a 2% false positive rate
(2% of non-terroristic communications are wrongly flagged)
Select a random communication. Define events: \(T\) = terroristic, \(F\) = flagged.
- Write down all information you have about \(T\) and \(F\) using probability notation.
- Set up a contingency table.
- Across all communications, terroristic and non, what’s the probability that a communication is flagged? You can use the table for intuition but should also provide a rigorous proof using notation.
- Suppose PRISM flags a communication. What’s the probability that they’ve actually found a terrorist (as opposed to an innocent person)? NOTE: You can use the table for intuition but should also provide a rigorous proof using notation.
- Explain why \(P(T|F)\) is so small!
Solution
\(P(T) = 1/1000000\), \(P(F^c | T) = 0.01\), \(P(F|T^c) = 0.02\)
.
Setting \(T\) \(T^c\) Total \(F\) 0.00000099 0.01999998 0.02000097 \(F^c\) 0.00000001 0.97999902 0.97999903 Total 0.000001 0.999999 1 From the table: \(P(F) = 0.02000097\)
Rigorous proof:
\[\begin{split} P(F) & = P(F \cap T) + P(F \cap T^c) \\ & = P(F|T)P(T) + P(F|T^c)P(T^c) \\ & = 0.99*0.000001 + 0.02*0.999999 \\ & = 0.02000097 \\ \end{split}\]From the table: \(P(T|F) = 0.00000099 / 0.02000097 \approx 0.0000494976\)
Rigorous proof:
\[\begin{split} P(T|F) & = \frac{P(F \cap T)}{P(F)} \\ & = \frac{P(F | T) P(T)}{P(F)} \\ & = \frac{0.99*0.000001}{0.02000097} \\ & = 0.0000494976 \\ \end{split}\]
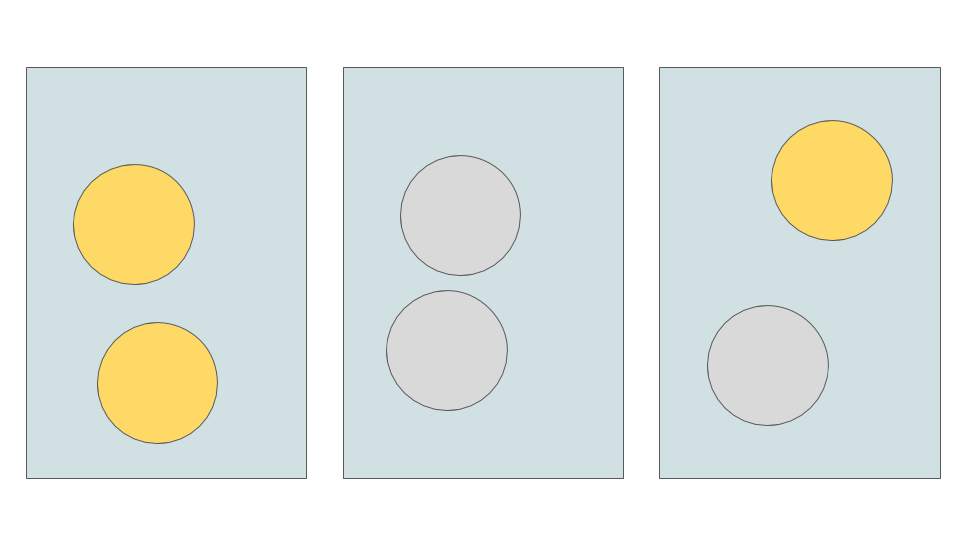
- Coins in drawers
A desk has 3 drawers:- drawer 1 contains 2 gold coins;
- drawer 2 contains 2 silver coins; and
- drawer 3 contains 1 gold coin & 1 silver coin.
- A classic problem: Monty Hall
In this exercise, you’ll solve one of the most well-known probability puzzles. On the game show Let’s Make a Deal, a contestant would be presented with three closed doors. Behind one door was a good prize (eg: a car). Behind the other two doors were undesirable ‘prizes’ (eg: goats). Here’s the game:- The contestant chooses a door (which remains closed).
- Monty Hall, the host, reveals an undesirable prize behind one of the other 2 doors. NOTE: If the contestant chooses the prize door, Monty randomly picks one of the others to open. If the contest chooses one of the bad doors, Monty reveals the other bad door.
- The contestant decides: stay with original door or switch to the unopened door?
PAUSE: Take some time to play this game! at http://www.shodor.org/interactivate/activities/SimpleMontyHall/
A reader asked Marilyn vos Savant (IQ = 228 and writer of “Ask Marilyn”) what the best strategy is: stay, switch, or it doesn’t matter? Marilyn gave the correct answer. BUT!
- More than 1000 PhDs disagreed with Marilyn’s answer & use of Bayes’ Rule. Some quotables include “How many irate mathematicians are needed to change your mind?” and “You blew it.” Even Paul Erdos didn’t believe until he ran a simulation. Read more terrible comments here.
- Who’s smarter than humans? Pigeons! Researchers compared the success of pigeons and humans by trial and error. After the trial, pigeons had learned to adopt the best strategy 96% of the time. However, the students had not found the best strategy even after 200 trials of practice each.
YOU TRY: What’s the best strategy? Stay, switch, or it doesn’t matter? In your solution, call your door “Door 1”, the door that Monty opens “Door 2”, & the unopened third door “Door 3”.