19 Continuous: joint & conditional models
19.1 Discussion
Let \(X\) and \(Y\) denote the proportions of time in one work week that employees A and B spend on task, respectively. Suppose the joint behavior of \(X\) and \(Y\) can be modeled by \[f_{X,Y}(x,y) = 2x \;\; \text{ for } 0 \le x \le 1, \; 0 \le y \le 1 \; .\]
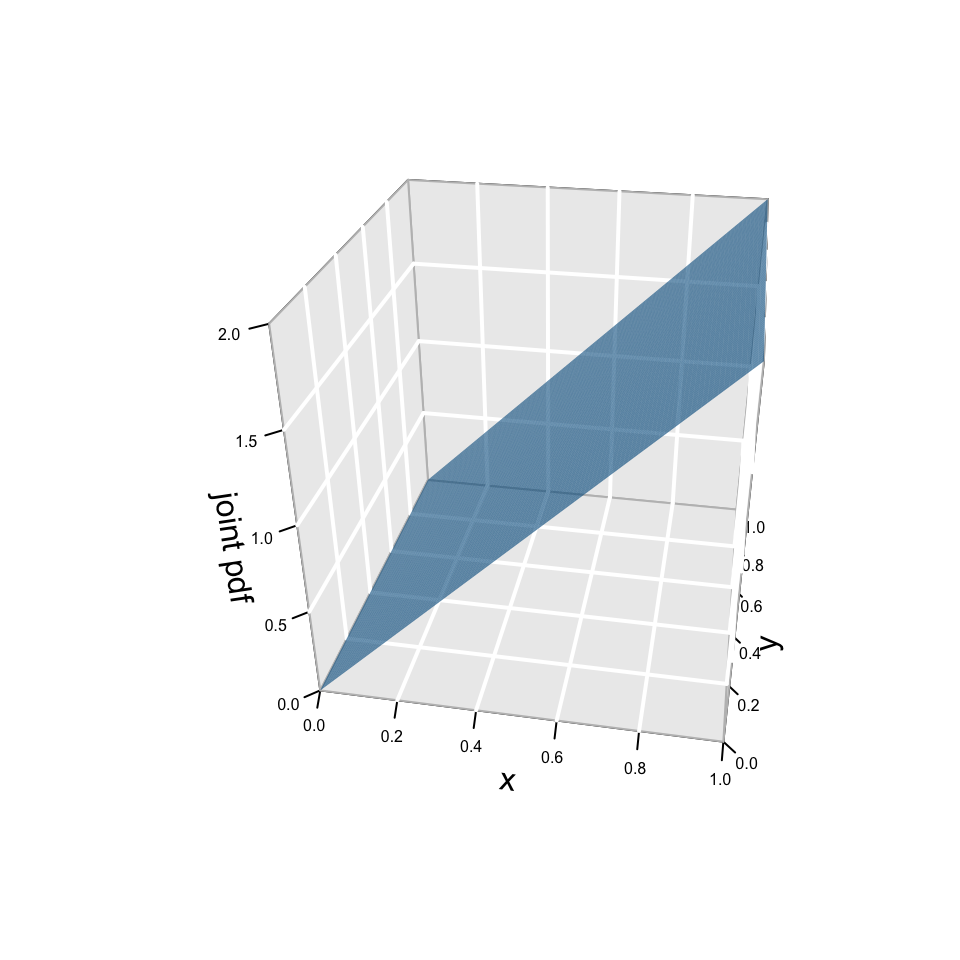
This pdf is a theoretical representation of the reality we observe day after day:
EXAMPLE 1: joint intuition
- How can we tell if \(f_{X,Y}(x,y)\) is a valid joint pdf?
- How can we use the joint pdf to calculate the probability that, in a given week, both A and B spend less than 50% of their time on task?
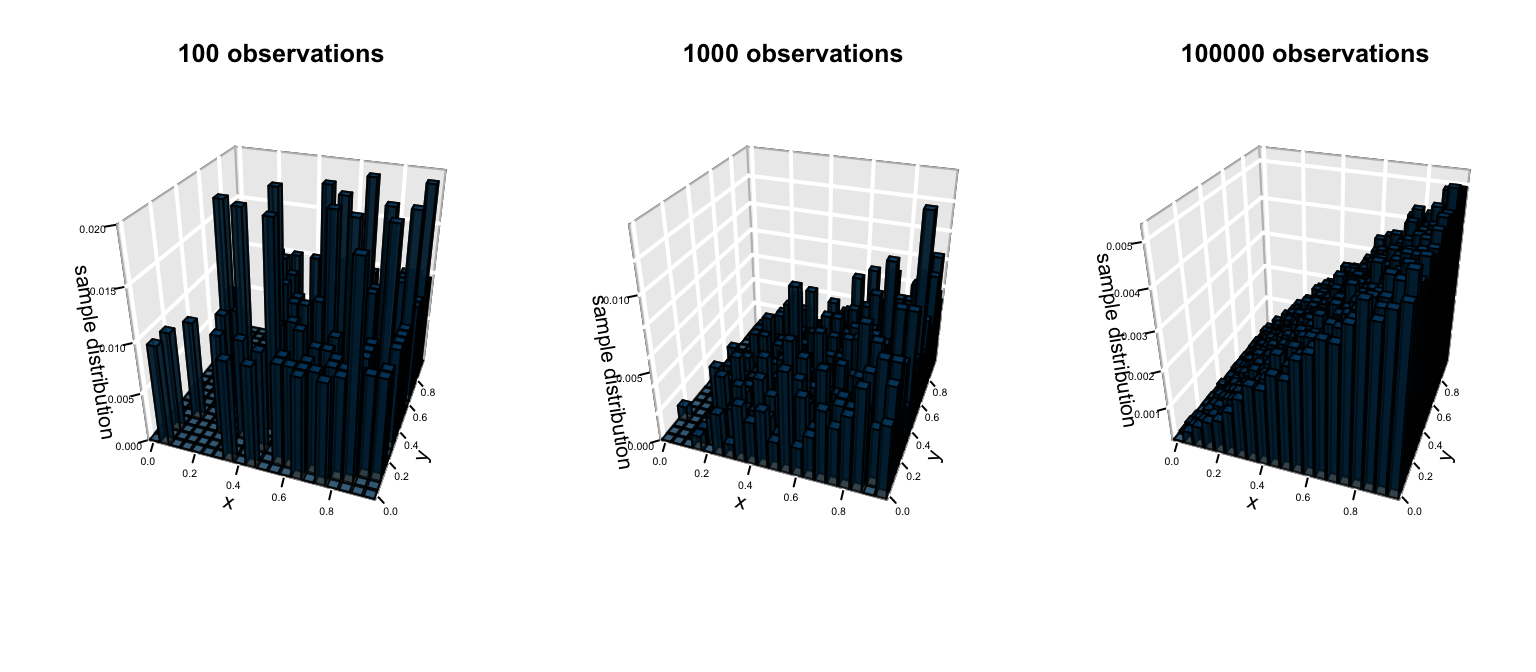
EXAMPLE 2: marginal intuition
Use the plot of the joint pdf to develop an understanding about the marginal behaviors of \(X\) and \(Y\). How might we specify these marginal models?
Joint models - Continuous RVs
The simultaneous behavior of \(X\) and \(Y\) is described by their joint pdf \[f_{X,Y}(x,y)\] where
- \(f_{X,Y}(x,y) \ge 0\) for all \(x,y\)
- \(\int \int f_{X,Y}(x,y) dx dy = 1\)
- \(f_{X,Y}(x,y)\) measures the density, NOT probability, at \((x,y)\)
- Given the joint behavior of \(X\) & \(Y\), we can find their marginal behaviors using the Law of Total Probability!: \[\begin{split} f_X(x) & = \int f_{X,Y}(x,y)dy \\ f_Y(y) & = \int f_{X,Y}(x,y)dx \\ \end{split}\]
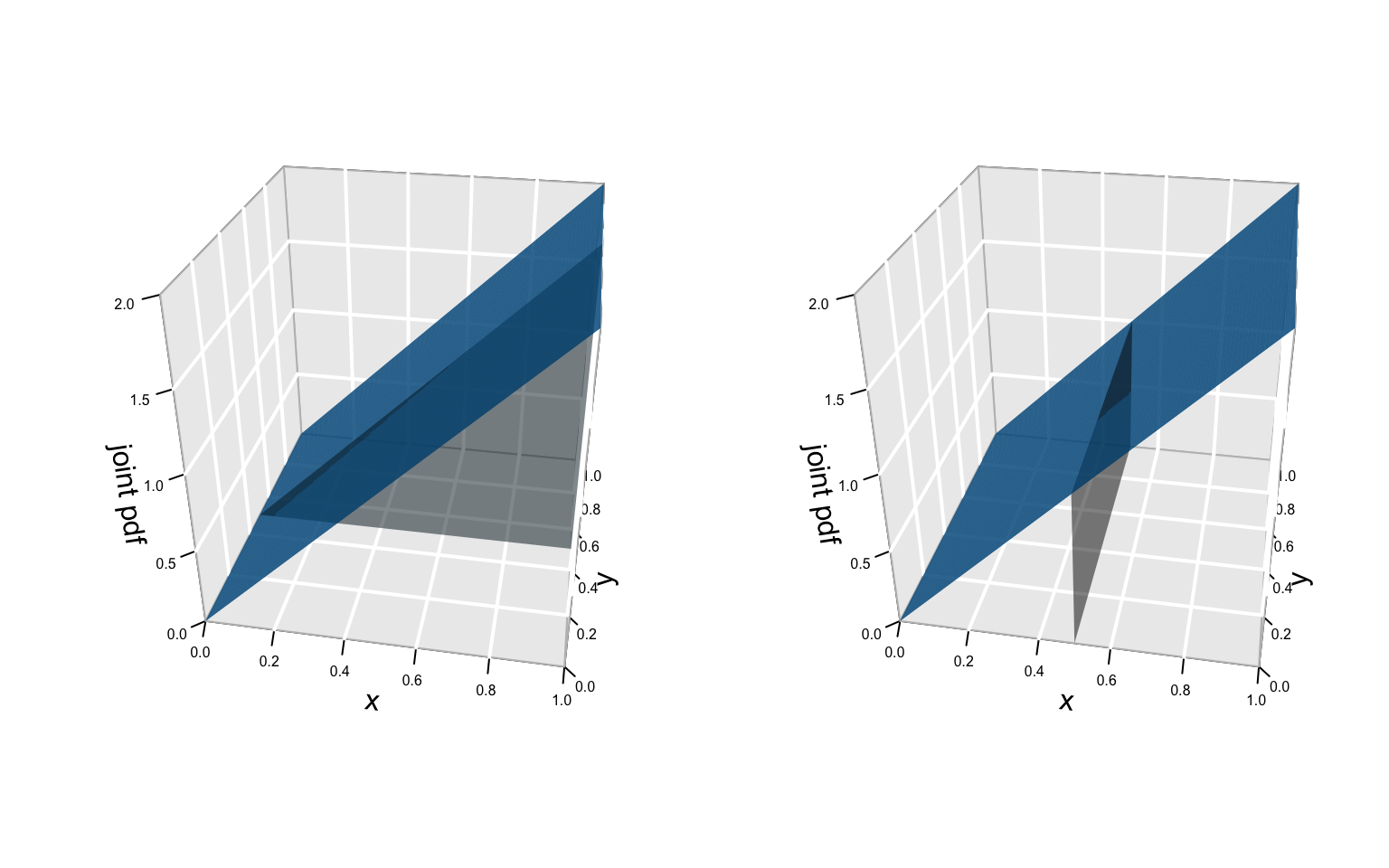
EXAMPLE 3: conditional
What’s your intuition about the conditional behavior of \(X\) when \(Y=0.5\) (left) is known? What about the conditional behavior of \(Y\) when \(X=0.5\) (right) is known? How might we specify the conditional pdfs of \(X\) and \(Y\)?
Conditional models - Continuous RVs
The conditional behavior of \(Y\) given that we observe \(X=x\) is described by the conditional pdf \[f_{Y|X=x}(y|x)\] where
- \(f_{Y|X=x}(y|x) \ge 0\) for all \(x,y\)
- \(\int f_{Y|X=x}(y|x) dy = 1\)
- \(f_{Y|X=x}(y|x)\) measures the conditional density, NOT probability, at \(y\)
- Given the joint & marginal behaviors of \(X\) & \(Y\), we can find their conditional behaviors: \[\begin{split} f_{Y|X=x}(y|x) & = \frac{f_{X,Y}(x,y)}{f_X(x)} \end{split}\]
\(X\) and \(Y\) are independent if and only if \[\begin{split} f_{Y|X=x}(y|x) & = f_Y(y) \\ f_{X,Y}(x,y) & = f_X(x)f_Y(y) \\ \end{split}\]
NOTE: These statements are equivalent. You only need to check one of them!
19.2 Exercises
- Joint
- Prove that \(f_{X,Y}(x,y) = 2x\) for \(0 \le x \le 1, \; 0 \le y \le 1\) is a valid joint pdf.
- Use the joint pdf to calculate the probability that, in a given week, both A and B spend less than 50% of their time on task.
Solution
\(f_{X,Y}(x,y) \ge 0\)
\(\int_0^1\int_0^1 2x dxdy = \int_0^1 1 dy = 1\)- \(\int_0^{0.5}\int_0^{0.5} 2x dxdy = \int_0^{0.5} 0.25 dy = 0.125\)
Marginal
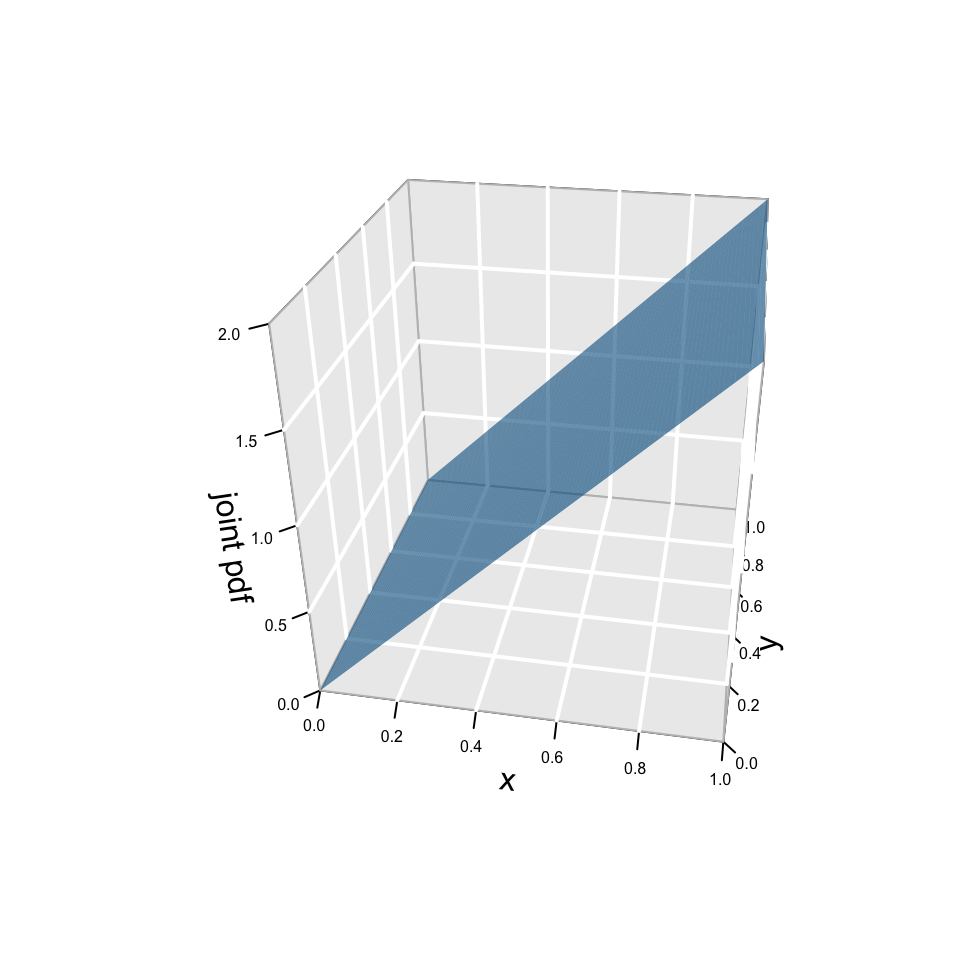
Derive the marginal pdfs of \(X\) and \(Y\), \(f_X(x)\) and \(f_Y(y)\), from the joint pdf \(f_{X,Y}(x,y) = 2x\) for \(0 \le x \le 1, \; 0 \le y \le 1\). These are plotted below: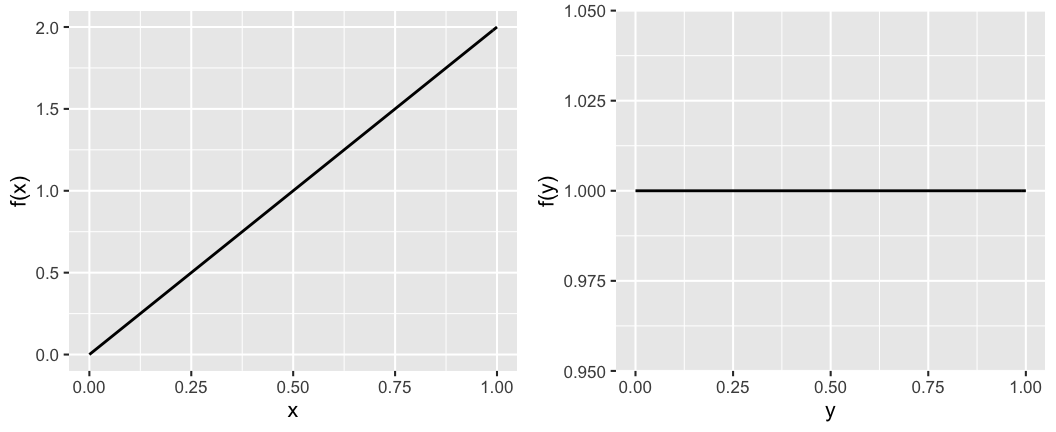
Solution
\[\begin{split} f_X(x) & = \int_0^1 2x dy = 2x \int_0^1 1 dy = 2x \\ f_Y(y) & = \int_0^1 2x dx = 1 \\ \end{split}\]
Conditional
Some conditional intuition is provided in the plots below.Derive and sketch the conditional pdf of \(X\) given \(Y=0.5\), \(f_{X|Y=0.5}(x|y=0.5)\).
For any given \(y\), derive and sketch the conditional pdf of \(X\) given \(Y=y\), \(f_{X|Y=y}(x|y)\).
Are \(X\) and \(Y\) independent RVs? Explain.
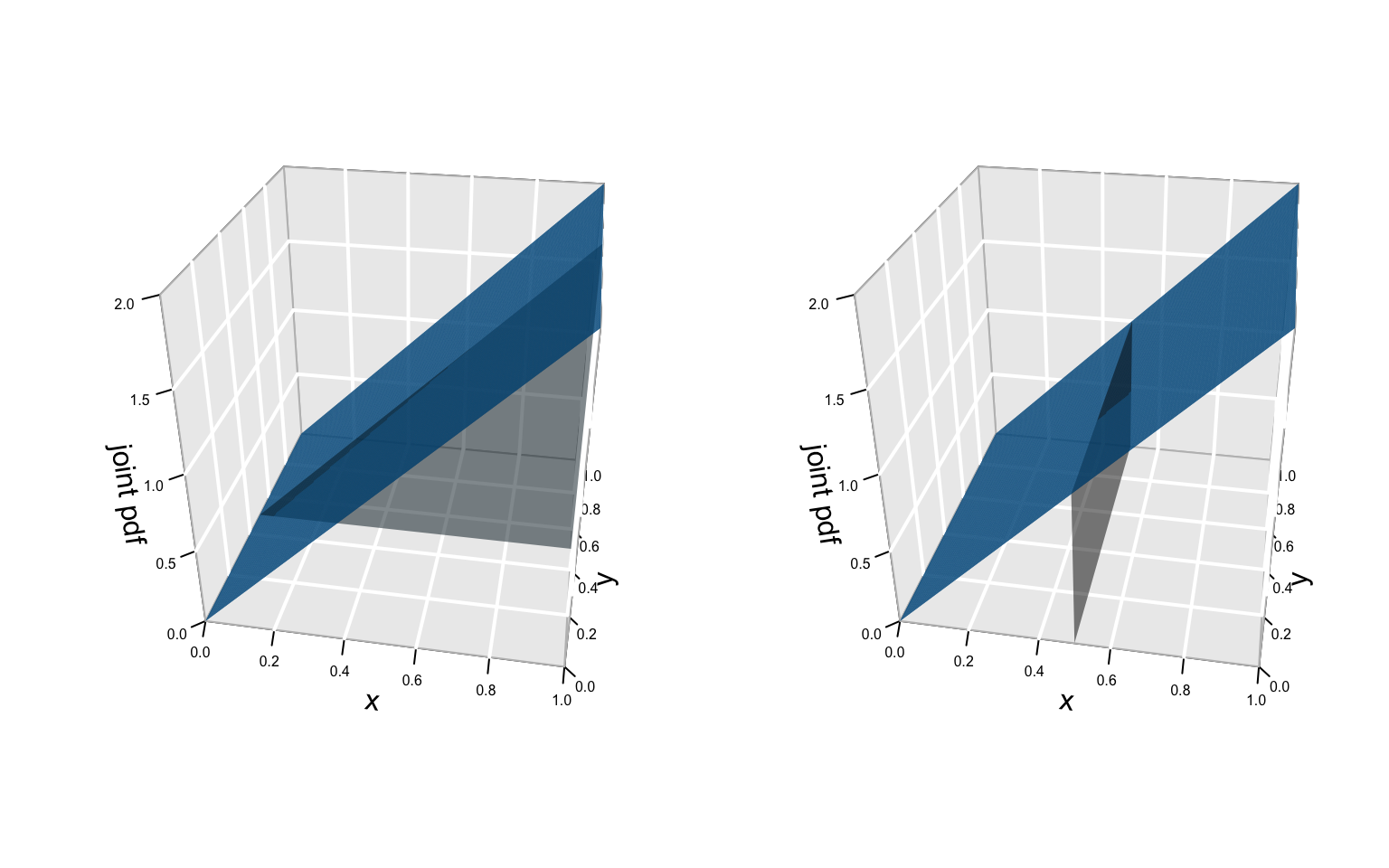
Solution
.
\[\begin{split} f_{X|Y=0.5}(x|y=0.5) & = \frac{f_{X,Y}(x,0.5)}{f_Y(0.5)}\\ & = \frac{2x}{1}\\ & = 2x \\ \end{split}\].
\[\begin{split} f_{X|Y=y}(x|y) & = \frac{f_{X,Y}(x,y)}{f_Y(y)}\\ & = \frac{2x}{1}\\ & = 2x \\ \end{split}\]Yes. \(f_{X|Y}(x|y) = f_X(x)\). Info about \(Y\) doesn’t change our understanding of \(X\).
- Independence
Are \(X\) and \(Y\) independent?- \(f_{X,Y}(x,y) = 6e^{-2x-3y}\) for \(x,y>0\)
- \(f_{X,Y}(x,y) = 1\) for \(x \in (0,1)\) and \(y \in (0,1)\)
- \(f_{X,Y}(x,y) = 1\) for \(0 < y < x < \sqrt{2}\)
Solution
- Yes. \(f_{X,Y}(x,y) = 6e^{-2x-3y} = 2e^{-2x} * 3e^{-3y} = f_X(x)f_Y(y)\)
- Yes. \(f_{X,Y}(x,y) = 1 = 1*1 = f_X(x)f_Y(y)\)
- No. The fact that the possible values of \(X\) are constrained by the values of \(Y\) tells us that information about \(Y\) will certainly change our understanding of \(X\).